|
一、一周知识概述
1、一次函数与一元一次方程、一元一次不等式
2、一次函数与二元一次方程(组)
二、重、难点知识归纳
1、一元一次方程与一次函数的关系
任何一元一次方程都可以转化为ax+b=0 (a, b为常数,a≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值.从图象上看,相当于已知直线y=ax+b确定它与x轴的交点的横坐标的值.
2、一次函数与一元一次不等式的关系
任何一个一元一次不等式都可以转化为ax+b>0或ax+b<0 (a, b为常数,a≠0)的形式,所以解一元一次不等式可以看作:当一次函数值大(小)于0时,求自变量的取值范围.
3、规律总结
一次函数y=kx+b与一元一次方程kx+b=0和一元一次不等式的关系:函数y=kx+b的图象在x轴上的点所对应的自变量x的值,即为不等式kx+b>0的解集;在x轴上所对应的点的自变量的值即为方程kx+b=0的解;在x轴下方所对应的点的自变量的值即为不等式kx+b<0的解集.
4、一次函数与一次方程(组)
(1)以二元一次方程ax+by=c的解为坐标的点组成的图象与一次函数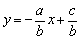 的图象相同. 的图象相同.
(2)二元一次方程组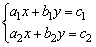 的解可以看作是两个一次函数 的解可以看作是两个一次函数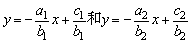 的图象的交点. 的图象的交点.
5、一次函数与方程(组)的应用
在实际生活中,如何应用函数知识解决实际问题,关键是建立函数模型,即列出符合题意的函数解析式,再利用方程(组)求解.
三、典型例题剖析
例1、某市电力公司为了鼓励居民用电,采用分段计费的方法计算电费:每月用电不超过100度,按每度0.57元计费;每月用电超过100度,前100度仍按原标准收费,超过部分按每度0.50元计费.
(1)设月用x度电时,应交电费y元,当x≤100和x>100时,分别写出y (元)关于x (度)的函数关系式;
(2)小王家第一季度交纳电费情况如下:
月份 |
一月份 |
二月份 |
三月份 |
合计 |
交费金额 |
76元 |
63元 |
45元6角 |
184元6角 |
问:小王家第一季度用电多少度?
分析:
(1)当x≤100时,费用为0.57元,当x>100时,
前100度应交电费100×0.57=57元,
剩下的(x-100)度应交电费0.50 (x-100).
(2)从交费情况看,一、二月份用电均超过100度,三月份用电不足100度.
解:
(1)当x≤100时,y=0.57x,
当x>100时,y=0.5x+7。
(2)显然一、二月份用电超过100度,三月份用电不足100度,
故将y=76代入y=0.5x+7中得x=138(度)
将y=63代入y=0.5x+7中,得x=112(度)
将y=45.6代入y=0.57x中,得x=80(度)
故小王家第一季度用电138+112+80=330(度).
例2、用画函数图象的方法解不等式:
-2x+3<3x-7.
分析:
由一次函数与一元一次不等式的关系可先将其化为一般形式,
再画图求解;也可以将-2x+3与3x-7看作是两个
关于x的一次函数,即y1=-2x+3,y2=3x-7。
于是不等式的解集即对应着y1<y2时自变量的取值.
解法1:
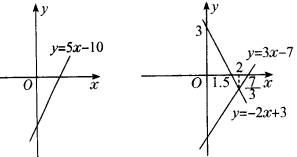
原不等式化为5x-10>0,画出直线y=5x-10如图所示,
可以看出x>2时这条直线上的点在x轴上方,
即这时y=5x-10>0,所以不等式的解集为x>2.
解法2:
将原不等式的两边分别看作是两个一次函数,
画出直线l1︰y=-2x+3,y2=3x-7,如图所示,
可以看出它们的交点的横坐标为2,当x>2时,
对于同一个x,直线y=-2x+3上的点在直线y=3x-7上相应的点的下方,这时-2x+3<3x-7,所以不等式的解集为x>2.
例3、某商场计划投入一笔资金采购一批紧俏商品,经过市场调查发现,如果月初出售,可获利15%,并可用本和利再投资其他商品,到月末又可获利10%;如果月末出售,可获利30%,但要付出仓储费用700元,请根据商场情况,如何购销获利较多?
分析:
由于题设中商场投资情况是未知的,不能直接比较,应根据投资情况列函数解析式,分类进行比较判断.
解:
设商场投资x元,在月初出售,到月末可获利y1元,
在月末出售,可获利y2元,则
y1=15%x+10% (x+15%x) =0.265x
y2=0.3x-700。
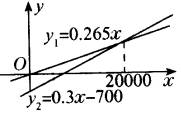
利用函数图象比较大小,在直角坐标系中,
作出两函数的图象如图所示,得两图象的交点坐标为(20000,5300).
由图象知当x>20000时,y2>y1.
当x=20000时,y1=y2;当x<20000时,y2<y1.
例4、用作图象的方法解方程组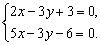
分析:
用图象法解二元一次方程组的关键是要作出两个二元一次方程表示的函数的图象,找出它们的交点.
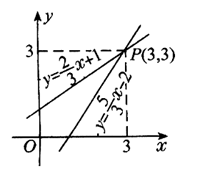
解:
由2x-3y+3=0得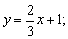
由5x-3y-6=0得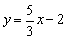 . .
在同一直角坐标系中作出直线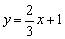 和 和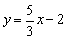 的图象, 的图象,
如图所示,得交点(3,3)
所以方程组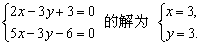
例5、哈尔滨市移动通讯公司开设了两种通讯业务:全球通使用者先缴50元基础费,然后每通话1分钟付话费0.4元;神州行不交月基础费,每通话1分钟付话费0.6元,若设一个月内通话x分钟,两种通讯方式的费用分别为y1元和y2元,那么
(1)写出y1、y2与x之间的函数关系式;
(2)在同一直角坐标系中画出两函数的图象;
(3)求出或寻求出一个月内通话多少分钟,两种通讯方式费用相同;
(4)若某人预计一个月内使用话费200元,应选择哪种通讯方式较合算.
分析:
(1)全球通的费用应为两种费用的和,即月基础费和通话费,神州行的费用应为通话费用;(2)运用描点法画图,但应注意自变量的取值范围;(3)可利用方程组求解,也可以根据图象回答;(4)寻求出当函数值为200元时,哪个函数所对应的自变量的值较大.
解:
(1)y1=50+0.4x (x≥0),y2=0.6x (x≥0)。
(2)图象如图所示.
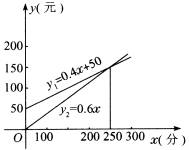
(3)根据图中两函数图象的交点所对应的横坐标为250,所以在一个月内通话250分钟时,两种通讯方式的收费相同.
另解:
当y1=y2时,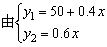 得x=250, 得x=250,
即当通话250分钟时,两种通讯方式的收费相同.
(4)当通话费为200元时,由图象可知,y1所对应的自变量的值大于y2所对应的自变量的值。即选取全球通更合算.
另解:当y1=200时有0.4x+50=200, ∴x1=375;
当y2=200时有0.6x=200, 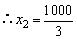 。 。
显然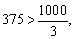 ∴选用全球通更合算。 ∴选用全球通更合算。
例6、随着教学手段不断更新,要求计算器进入课堂.某电子厂家经过市场调查,发现某种计算器的供应量x1(万个)与价格y1(万元)之间的关系如图中供应线所示,而需求量x2(万个)与价格y2(万元)之间的关系如图中需求线所示.如果你是这个电子厂厂长,应计划生产这种计算器多少个?每个售价多少元,才能使市场达到供需平衡?
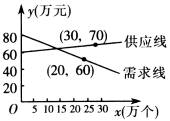
解:
设供应线的函数解析式为y1=k1x+b1,需求线的函数解析式为y2=k2x+b2,由图象知,y1的图象过点(0,60),(30,70)两点,求得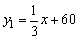 ,同理求得y2=-x+80,令y1=y2得x=15,故生产这种计算器15万件,每个售价65元,才能使市场达到供需平衡. ,同理求得y2=-x+80,令y1=y2得x=15,故生产这种计算器15万件,每个售价65元,才能使市场达到供需平衡.
- 返回 -
|