一、一周知识概述

1、轴对称变换

　　由一个平面图形可以得到它关于一条直线l对称的图形．这个图形与原图形的形状、大小完全一样，且新图形上的每一个点，都是原图上某一点关于直线l的对称点．

　　像这样，由一个平面图形得到它的轴对称图形叫做轴对称变换．

指出：

　　（1）成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到的．

　　（2）由线段的垂直平分线的性质还可知连接任意一个对对应点的线段被对称轴垂直平分．

2、直角坐标系中关于x轴、y轴的对称点的特征

　　（1）点(x,y)关于x轴对称的点的坐标是(x,－y)，即关于x轴对称的点的横坐标相同，纵坐标互为相反数．

　　（2）点(x,y)关于y轴对称的点的坐标是(－x,y)，即关于y轴对称的点的纵坐标相同，横坐标互为相反数．

指出：

　　（1）关于坐标轴对称的点的坐标仅只有符号不同，其绝对值分别相同，这是因为一对对称点到坐标轴的距离始终都是相等的，仅就只是所处的象限不同．

　　（2）根据对称点的特征可知：在直角坐标系中作出一个几何图形关于坐标轴对称的图形只需作出某些点的对称点即可.

3、直角坐标系中，关于某条直线对称的点的特征

　　（1）点(a,b)关于直线x=m对称点的坐标是(2m－a,b)；

　　（2）点(a,b)关于直线y=n对称的点的坐标是(a,2n－b)．

指出：

　　（1）直线x＝m是过(m,0)且垂直于x轴的直线，该直线任何一点的横坐标是m．

　　（2）直线y＝n是过(0,n) 且垂直于y轴的直线，该直线上任何一点的纵坐标是n．

二、重难点知识概述

　　轴对称变换的概念，关于x轴、y轴，直线x=m，直线y=n对称点的特征．

三、典型例题剖析

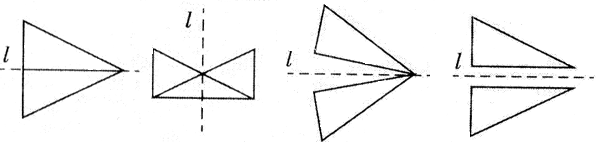
例1、两个全等的三角板，可以拼出各种不同的图形，如图，已画其中一个三角形，请你分别补出另一个与其全等的三角形，使每个图形分别成不同的轴对称图形（所画的三角形可与原三角形有重叠部分）．

分析：已知一个三角形，使与之全等的三角形构成轴对称图形，其关键是确定对称轴，由于有无数条对称轴，所以所作的轴对称图形有无数种情形.

解：如图所示

例2、在下图中，分别作出点P关于OA，OB的对称点P1，P2，连接P1、P2交OA于M，交OB于N，若P1P2=5cm，则△PMN的周长为多少？

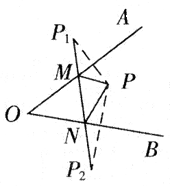
分析：求△PMN的周长即是求PM＋PN＋MN．因为P，P1关于OA对称，P，P2关于OB对称，所以PM=P1M，PN=P2N，因而PM＋PN＋MN＝P1M＋MN＋P2N．

解：∵P1是P关于OA的对称点，P2是P关于OB的对称点，

　　∴PM=P1M，PN=P2N，

　　∴PM＋PN＋MN＝P1M＋MN＋P2N＝P1P2＝5cm，

　　∴△PMN的周长是5cm．

例3、如图所示，A、B两点在l的两侧，在l上找一点C，使C到A、B的距离之差最大．

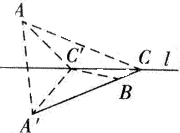
分析：以l为对称轴作A点的对称点A′，作直线A′B交l于C点，则C为所求作的点．

证明：在l上异于C点，找一点C′，连接C′A，C′B

　　　∵A，A′关于l轴对称，

　　　∴l为AA′的垂直平分线，则CA=CA′．

　　　∴CA－CB=CA′－CB=A′B．

　　　又∵C′在l上，

　　　在△A′BC′中，C′A′－C′B<A′B，

　　　∴C′A′－C′B<CA－CB．

例4、如图，四边形ABCD的四个顶点坐标分别为A（－5，1）、B（－2，1）、C（－2，5）、D（－5，4），分别作出与四边形ABCD关于y轴和x轴对称的图形．

分析：要作出四边形ABCD关于y轴的对称图形，只需分别作点A、B、C、D关于y轴的对称点即可．同理可作出关于x轴的对称图形．

解：点(x,y)关于y轴对称的点的坐标为(－x,y)，因此四边形ABCD的顶点A、B、C、D关于y轴的对称的点分别为A′（5，1）、B′（2，1）、C′（2，5）、D′（5，4）．依次连接A′B′，B′C′，C′D′，D′A′，就可得到与四边形ABCD关于y轴对称的四边形A′B′C′D′．

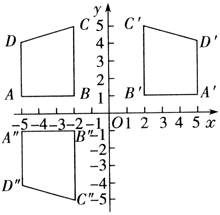
同理可知四边形ABCD的顶点A、B、C、D关于x轴的对称点分别为A″（－5，－1）、B″（－2，－1）、C″（－2，－5）、D″（－5，－4）．依次连接A″B″、B″C″、C″D″、D″A″，就可得到四边形ABCD关于x轴对称的四边形A″B″C″D″．

例5、如图，已知△ABC的顶点坐标分别为A（－4，1），B（－1，－1），C（－3，2），试作出△ABC关于直线x=2的轴对称图形．

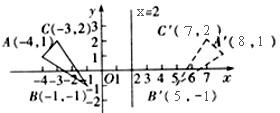
分析：要作出△ABC关于直线x=2对称的三角形，其关键是作出△ABC的三个顶点A、B、C关于直线x=2的对称点．

解：因为点(a,b)关于直线x＝2的对称点是：(2x－a,b)，所以△ABC的顶点A、B、C关于直线x=m的对称点A′（8，1），B′（5，－1），C′（7，2）．顺次连接△A′B′、B′C′、C′A′，即可得到△ABC关于直线x=m对称的三角形A′B′C′．

例6、求直线y=2x－1关于x轴对称的直线的解析式．

分析：求一条直线关于x轴对称的直线，可以从已知直线上任取两点，求出其坐标，再求出这两点关于x轴的对称点的坐标，再利用待定系数法求对称直线的解析式．

解：当x=0时，y=－1；当x=1时，y=1即直线y=2x－1过A（0，－1），B（1，1）两点．这两个点关于x轴的对称点分别为A′（0，1），B′（1，－1），则直线A′B′与直线AB关于x轴对称．设直线A′B′的解析式为y=kx＋b，把（0，1）（1，－1）代入上式，得所以直线A′B′的解析式为y=－2x＋1．

- 返回 -