1、单项式
⑴单项式:像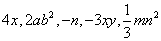 ,它们都是数或字母的积,这样的式子叫做单项式,单独的一个数或一个字母也是单项式。
,它们都是数或字母的积,这样的式子叫做单项式,单独的一个数或一个字母也是单项式。
⑵单项式的系数:单项式中的数字因数叫做单项式的系数。如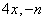 的系数分别是4和-1。
的系数分别是4和-1。
⑶单项式的次数:一个单项式中所有字母的指数和叫做这个单项式的次数。如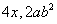 的次数分别是1和3。
的次数分别是1和3。
指出:
⑴单项式中的数与字母或字母与字母之间都是乘积关系,如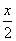 可以看成是
可以看成是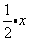 ,所以
,所以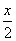 是单项式,而
是单项式,而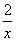 就不是单项式。
就不是单项式。
⑵如果一个单项式只含有字母因数,它的系数是1或-1。
⑶单项式中若字母没写指数时,它的次数是1,而不是0,如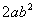 中字母
中字母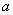 的指数是1,不是0。
的指数是1,不是0。
2、多项式
⑴多项式:几个单项式的和叫做多项式,在多项式中每个单项式叫做多项式的项,其中,不含字母的项叫做常数项,一个多项式有几项就叫做几项式。
⑵多项式的次数:多项式里,次数最高的项的次数就是这个多项式的次数。
指出:
⑴多项式的每一项都包括它前面的符号,如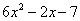 第一项是
第一项是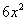 ,第二项是
,第二项是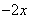 ,而不是
,而不是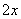 ,常数项是-7,而不是7。
,常数项是-7,而不是7。
⑵由于多项式是由单项式组成,每一个单项式的次数就是各项的次数,多项式的次数仅指次数最高的那个单项式的次数,即多次式的次数就高不就低。
3、整式
整式:单项式和多项式统称整式,即
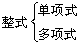
4、同类项
⑴同类项:所含字母相同,并且相同字母的次数也相同的项叫做同类项,几个常数项也是同类项。
⑵合并同类项:把多项式中的同类项合并成一项,即把它们的系数相加作为新的系数,而字母部分不变,叫做合并同类项。
指出:
⑴判断几个单项式(或多项式中的项)是否是同类项有两个条件:①所含字母相同;②相同字母的指数分别相同,同时具备这两个条件者是同类项,二者缺一不可。
⑵同类项与系数无关,与字母的排列无关。
⑶几个常数项也是同类项。
⑷合并同类项应注意:①只能把同类项合并成一项,不是同类项不能合并;②如果两个同类项的系数互为相反数,合并同类项后,结果为0;③只要不再有同类项,就是最后结果,结果可能是单项式,也可能是多项式。
5、整式的加减
几个整式相加减,通常用括号把每一个整式括起来,再用加减号连接;然后去括号,合并同类项。
指出:
⑴整式加减的一般步骤归纳为三步:①列出算式;②去括号;③合并同类项。
⑵整式加减的实质就是合并同类项。
应用整式的加减进行化简求值,一般先将代数式进行去括号、合并同类项,再代入字母的值进行计算,可简单地记为“一化二代三算”。
例1、指出下列各代数式中的单项式,并写出各单项式的系数和次数:
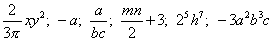 。
。
分析:
判定一个代数式是否是单项式,关键就是看式子中的数与字母或字母与字母之间是不是乘积关系,如果含有加、减、除的关系,那么它就不是单项式。
解:
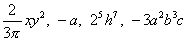 是单项式。
是单项式。
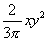 的系数是
的系数是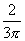 ,次数是3。
,次数是3。
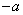 的系数是-1,次数是1。
的系数是-1,次数是1。
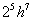 的系数是
的系数是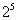 ,次数是7。
,次数是7。
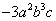 的系数是-3,次数是6。
的系数是-3,次数是6。
例2、下列代数式,哪些是多项式,并指出它是几次几项式。
⑴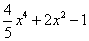 ; ⑵
; ⑵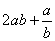 ;
;
⑶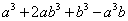 ; ⑷
; ⑷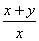 。
。
分析:
⑴判断一个代数式是不是多项式,首先根据多项式的概念,考虑它是不是几个单项式的和。
⑵判断一个多项式是几次几项式,首先看哪一项的次数最高,这一项的次数就是这个多项式的次数,再看这个多项式所含的项数,有几项就是几项式。
解:
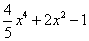 ,
,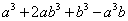 是多项式;
是多项式;
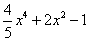 是四次三项式;
是四次三项式;
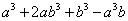 是四次四项式。
是四次四项式。
例3、把下列各代数式填入相应的大括号里:
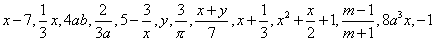 。
。
单项式集合:{ };
多项式集合:{ };
整式集合:{ }。
分析:
分母中含有字母的式子,一定不是单项式,也不是多项式,所以它也一定不是整式,故首先应排除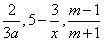 ,再根据是否含有加减运算来判别它们是单项式还是多项式。
,再根据是否含有加减运算来判别它们是单项式还是多项式。
解:
单项式集合: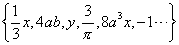
多项式集合: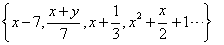
整式集合: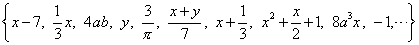
例4、⑴已知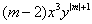 是关于
是关于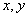 的六次单项式,求字母
的六次单项式,求字母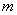 的值。
的值。
⑵多项式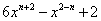 是关于
是关于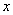 的三次三项式,求代数式
的三次三项式,求代数式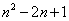 的值。
的值。
分析:
⑴由单项式的次数的定义可知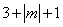 应等于6,解此方程即可求出
应等于6,解此方程即可求出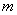 的值,另注意
的值,另注意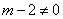 。
。
⑵应分类讨论,即当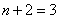 和
和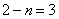 都满足题意。
都满足题意。
解:
⑴因为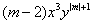 是关于
是关于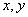 的六次单项式,所以
的六次单项式,所以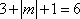 ,解得
,解得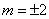 。
。
当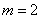 时,
时,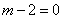 ,此单项式不是关于
,此单项式不是关于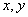 的六次单项式,故
的六次单项式,故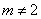 ,∴
,∴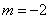 。
。
⑵当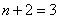 时,则
时,则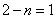 ,此时为三次三项式,所以当
,此时为三次三项式,所以当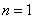 时,
时,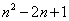 的值为0。
的值为0。
当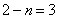 时,则
时,则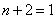 ,此时为三次三项式,所以当
,此时为三次三项式,所以当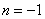 时,
时,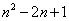 的值为4。
的值为4。
所以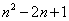 的值为0或4。
的值为0或4。
例5、合并下列多项式中的同类项:
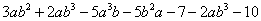
分析:
先找出多项式中的同类项,然后根据合并同类项的法则进行合并。
解:
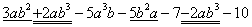
=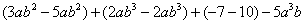
=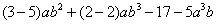
=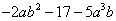
例6、计算
⑴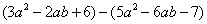 ;
;
⑵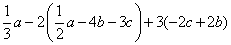
分析:
第⑴题按照基本步骤,先去括号,再合并同类项;第⑵题中有数乘多项式,先利用分配律将数乘遍各项,再去括号,合并同类项。
解:
⑴原式=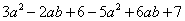
=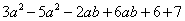
=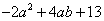
⑵原式=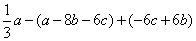
=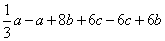
=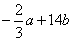
例7、已知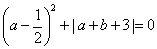 ,求代数式
,求代数式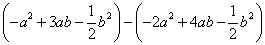 的值。
的值。
分析:
由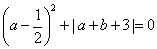 及
及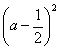 和
和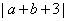 的非负性可得
的非负性可得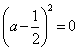 ,
,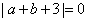 ,即
,即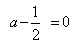 ,
,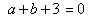 ,故
,故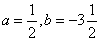 ,对于求代数式的值,只需按照化简求值的基本步骤解答。
,对于求代数式的值,只需按照化简求值的基本步骤解答。
解:
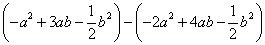
=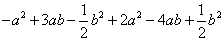
=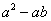
∵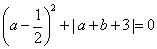
∴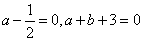
∴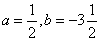
∴原式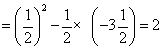
例8、如图是一个长方形娱乐场所,其宽为,长是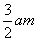 ,现要求这个娱乐场所有一半以上的绿地,小明提供了如图所示的设计方案,其中半圆形休息区和长方形游泳区以外的地方都是绿地,请你判定他的设计方案符合要求吗?
,现要求这个娱乐场所有一半以上的绿地,小明提供了如图所示的设计方案,其中半圆形休息区和长方形游泳区以外的地方都是绿地,请你判定他的设计方案符合要求吗?