1、平方差公式
两个数的和与这两个数的差的积等于这两个数的平方差，即(a＋b)(a－b) ＝a2－b2.
指出：
(1)平方差公式的特征：①左边是两个二项式相乘，并且这两个二项式中有一项完全相同，另一项互为相反数；②右边是乘式两项的平方差，并且是完全相同的项的平方减去互为相反数项的平方.
(2)运用公式时除了掌握其结构特征外，还应注意如下几点：①公式中的a，b具有广泛的含义，可以表示一个数、一个字母，一个单项式，还可以表示一个多项式；②运用公式时关键是识别两个数，哪个是完全相同的，哪个是互为相反数.
2、平方差在简便运算中的应用
当问题中的两因数不是两数和与两数差的积的形式时，可适当变形，使之符合公式的特点，从而能运用公式达到巧算的目的.
3、完全平方公式
两数和(或差)的平方，等于它们的平方和，加(或减)它们的积的2倍.
指出：
(1)完全平方公式的结构特征：①公式的左是两个相同的二项式相乘，即两个数和(或差)的平方；②公式的右边是一个三项式，其中两项是左边的二项的平方和，第三项是左边两项的积的2倍，但符号与左边的符号相同.
(2)公式中的字母具有一般性，它可以表示数也可以表示多项式.
4、乘法公式的变式及综合运用
(1)a2－b2＝(a＋b)(a－b);
(2)(a＋b)2－(a－b)2＝4ab;
(3)a2＋b2＝(a＋b)2－2ab＝(a－b)2＋2ab
指出：
(1)公式中的a，b既可以表示单项式，也可以表示多项式.
(2)乘法公式既可以单独使用，也可以同时使用.
(3)这些公式既可以正用，也可以逆用，因此在解题时应灵活地运用公式，以计算简捷为宜.
5、添括号
添括号时，如果括号前面是正号，括到括号里的各项都不变号；如果括号前面是负号，括到括号里的各项都改变符号.即a＋b＋c＝a＋(b＋c)，a－b－c＝a－(b＋c).
指出：
(1)添括号是添上括号和括号前面的符号，也就是说，添括号时，括号前面的“＋”号“－”号，也是新添的，不是原来多项式的某一项的符号“移”出来的.
(2)添括号时，首先要理解题目的要求，弄清楚要求括号前是“＋”号还是“－”号，然后再根据法则添括号，尤其要注意括号前面是“－”时，括到括号里面的各项都改变符号.
(3)去括号和添括号是两种相反的过程，因此可以相互检验.
例1、计算：
(1)(3a＋2b)(2b＋3a);
(2)(x－2y)(－x－2y);
(3)
;
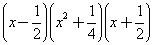(4)(a＋b＋c)(a－b－c)
分析：
相乘的两个二项式，只要它们有一项完全相同，另一项互为相反数，就符合平方差公式.相乘的结果是相同项的平方减去相反项的平方.
第(1)题的相同项是2b，相反项是3a与－3a.
第(2)题可以按第(1)题的方法计算，也可以先改变第二个因式的符号再运算.
第(3)题应先计算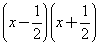
，恰好可以运用平方差公式，所得的积再与
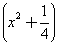相乘，又恰好能再用平方差公式计算.
第(4)题虽然不能直接运用平方差公式计算，但认真观察两个二项式中的相同项和相反项，就不难分组转化成平方差公式的结构形式.
解：(1)原式＝(2b＋3a)(2b－3a)
＝(2b)2－(3a)2
＝4b2－9a2
(2)原式＝(－2y＋x)(－2y－x)
＝(－2y)2－x2
＝4y2－x2
(3)原式＝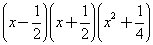
＝
＝
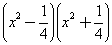
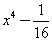
(4)原式＝[a＋(b＋c)][a－(b＋c)]
＝a2－(b＋c)2
＝a2－(b2＋2bc＋c2)
＝a2－b2－2bc－c2
例2、计算：
(1)98×102； (2)99×101×10001.
分析：
将98写成100－2，102写成100＋2，第(1)题即能用平方差公式计算；同理将99写成100－1，101写成100＋1，第(2)题也可用平方差公式计算：
解：(1)98×102
＝(100－2)(100＋2)
＝10000－4＝9996
(2)99×101×10001＝(100－1)(100＋1)×10001
＝(10000－1)(10000＋1)
＝100000000－1＝99999999
例3、计算：
(1)20042－19962
(2)(x－y＋z)2－(x＋y－z)2
分析：
由于2004与1996的和是一个特殊数，(x－y＋z)和(x＋y－z)的和为一个单项式，所以此类问题总是可逆用平方差公式.
解：(1)20042－19962
＝(2004＋1996)(2004－1996)
＝4000×8＝32000
(2)(x－y＋z)2－(x＋y－z)2
＝[(x－y＋z)＋(x＋y－z)][ (x－y＋z)－(x＋y－z)]
＝2x(－2y＋2z)＝－4xy＋4xz
例4、计算：
(1)(3x＋4y)2;
(2)(－3＋2a)2；
(3)(2a－b)2；
(4)(－3a－2b)2
分析：运用两数和的平方公式应正确理解公式的特征，公式的左边是一个二项式的平方，显然四个小题都可以用完全平方公式，在运用公式时注意分清是用两数和，还是两数差.
解：(1)原式＝(3x)2＋2·3x·4y＋(4y)2
＝9x2＋24xy＋16y2
(2)原式＝(－3)2＋2·(－3)·2a＋4a2
＝4a2－12a＋9
(3)原式＝(2a)2＋2·2a·(－b)＋(－b)2
＝4a2－4ab＋b2
(4)原式＝[－(3a＋2b)]2
＝(3a＋2b)2
＝(3a)2＋2·(3a)·2b＋(2b)2
＝9a2＋12ab＋4b2
例5、按下列要求，把多项式x2－y2＋2y－1的后三项用括号括起来：
(1)括号前面带有“＋”； (2)括号前面带有“－”号.
分析：
添括号时首先要弄清楚要求所添的括号前面带有“＋”号还是“－”号，其次要弄清楚要求把哪些项括到括号里.如果所添的括号前面带有“＋”号，那么括到括号里的各项不变号；如果所添的括号前面带有“－”号，那么括到括号里的各项都要改变符号.
解：(1)x2－y2＋2y－1＝x2＋(－y2＋2y－1)
(2) x2－y2＋2y－1＝x2－(y2－2y＋1)
例6、计算：
(1)(x－2y＋3z)(x＋2y－3z); (2)1022
分析：
第(1)题两个多项式不完全相同，不能直接运用完全平方式，但它符合平方差公式，再用完全平方公式；第(2)题，把102写成100＋2，可利用两数和的平方公式.
解：(1) (x－2y＋3z)(x＋2y－3z)
＝[x－(2y－3z)][x＋(2y－3z)]
＝x2－(2y－3z)2＝x2－(4y2－12yz＋9z2)
＝x2－4y2＋12yz－9z2
(2)1022
＝(100＋2)2
＝1002＋2×100×2＋22
＝10404
例7、计算下列各题：
(1)(－2x－7)(－2x＋7);
(2)(3x－y)(y＋3x)－2(4x－3y)(4x＋3y);
(3)(m＋1)2－5(m＋1)(m－1)＋3(m－1)2;
(4)(2x＋3y－1)(1＋2x－3y)＋(1＋2x－3y)2
解：(1)原式＝(－2x)2－72＝4x2－49
(2)原式＝(3x)2－y2－2(16x2－9y2)
＝9x2－y2－32x2＋18y2
＝－23x2＋17y2
(3)原式＝m2＋2m＋1－5m2＋5＋3m2－6m＋3
＝－m2－4m＋9
(4)原式＝[2x＋(3y－1)][2x－(3y－1)]＋[2x＋(1－3y)]2
＝4x2－(3y－1)2＋4x2＋4x(1－3y)＋[－(3y－1)]2
＝8x2－(3y－1)2＋4x－12xy＋(3y－1)2
＝8x2＋4x－12xy
