1、分式
一般地，如果A、B表示两个整式，并且B中含有字母，那么式子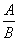
叫做分式．
分式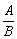
中，A叫做分子，B叫做分母．
2、分式有意义、无意义，分式的值为零的条件
分式有意义的条件是分式的分母不为0；
分式无意义的条件是分式的分母为0；
分式的值为0的条件是分子为0，且分母不为0．
3、分式的基本性质
分式的分子与分母同乘(或除)以一个不为零的整式，分式的值不变．用式子表示为：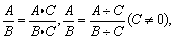
其中A、B、C为整式．
4、通分
与分数通分类似，利用分式的基本性质，使分式的分子分母同乘以适当的整式，不改变分式的值，化异分母分式为同分母分式，这样的分式变形叫做分式的通分．
5、约分
与分数的约分类似，利用分式的基本性质，约去分式的分子和分母的公因式，不改变分式的值，这样的分式变形叫做分式的约分．
6、分式的乘除法法则
分式乘分式，用分子的积作积的分子，分母的积作积的分母；
分式除以分式，把除式的分子、分母颠倒位置后与被除式相乘．
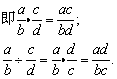
7、分式的乘方法则
分式乘方，把分子、分母各自乘方．即
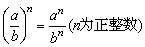
8、同分母的分式的加减法
同分母的分式相加减，分母不变，把分子相加减．
即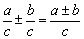
．
9、异分母分式加减法
异分母分式相加减，先通分，变为同分母分式，然后再加减．
即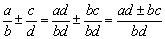
．
10、零指数幂的意义
任何不等于零的数的零次幂都等于1，即a0=1(a≠0)．零的零次幂没有意义．
11、负整数指数幂
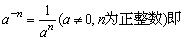
任何不等于零的数的－n(n为正整数)次幂等于这个数的n次幂的倒数．
12、负整数指数幂用正整数指数幂表示
在运用正整数指数幂表示负整数指数幂时，对代数式中的相关幂与积的乘方或幂的其他运算要先进行运算，并且正整数指数幂的运算对负整数指数幂的运算都适用．
13、科学记数法
(1)用科学记数法可以把绝对值较小的数表示成a×10－n(1≤|a|＜10，n为正整数)的形式．
(2)确定n的具体数值：通常从小数点往后至第一个不为零的数字上所有零的个数，包括小数点前面的那个零．
例1、使得分式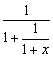
有意义的条件是（ ）
A．x≠0 B．x≠－1且x≠－2
C．x≠－1 D．x≠－1且x≠0
分析：
分式有意义应是使分式中的每一个分母都不为零．可采用验证的方法：当x=－1时，小分母1＋x=0．当x=－2时，大分母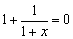
分式都无意义．故要使分式有意义，则必有x≠－1且x≠－2，也可以采用直接求解的方法．
解：
要使原分式有意义，
必须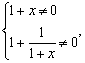
解得x≠－1且x≠－2
故，选B
例2、下列分式中，当x取何值时，分式有意义？当x取什么值时，分式的值为0？
．
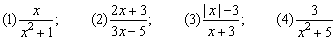分析：
分式有意义的条件是分母不为0，由此可求出x的值；分式的值为0的条件是分子等于0，而分母不为0．但必须明确，只有在分式有意义的前提下，才能讨论它的值是多少，本题就是要找到这样的数，使分式的分子等于0，而分母不等于0．
解：
(1)对于一切实数，x2≥0，∴x2＋1＞0．
∴当x为任意实数时，分式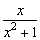
都有意义．
由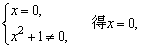
∴当x=0时，分式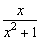
的值为0．
(2)由分母3x－5≠0，得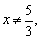
．
由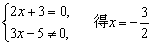
．
．
(3)由分母x＋3≠0，得x≠－3．
．
由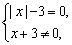
得x=3．
∴当x=3时，分式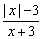
的值为0．
(4)因为对于一切实数x，x2≥0，∴x2＋5＞0．
所以当x为任何实数时，分式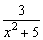
都有意义．
由于分子3不等于0，所以分式的值不可能为0，即这样的x值不存在．
例3、已知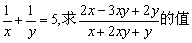
．
分析：
首先应排除一种错误的想法，即若试图从已知条件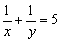
中求出x以及y的具体值，然后代入求值的分式，显然是行不通的．那么如何求值呢？待求的分式也不能化简，所以应该着眼于寻求已知与未知之间的“桥梁”即共同点，这就需要利用分式的基本性质把已知条件变形或将待求式变形，用整体代入法求值．
解法1：
由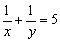
可知x≠0，y≠0，故在等式两边同乘以xy得
x＋y=5xy
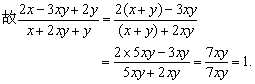
解法2：
∵xy≠0，将待求式的分子、分母同时除以xy，得
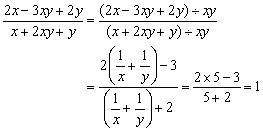
例4、计算：
．
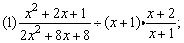
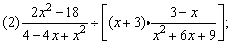
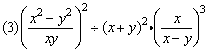分析：
(1)式是分式与整式的乘除混合运算，应先把分式的乘除法运算统一成乘法运算，再利用乘法运算法则进行计算．
(2)式也是分式与整式的乘除混合运算；并且有括号，所以应先算括号内的，再算括号外的．
(3)注意运算的顺序．
解：
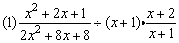
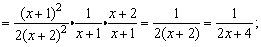
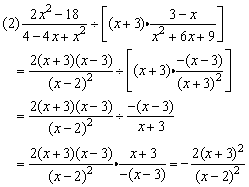
例5、计算：
．
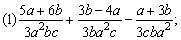
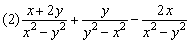分析：
(1)3a2bc=3ba2c=3cba2是同分母分式相加减，分母不变，把分子相加减，但应把各分子看成一个整体，用括号括起来，再相加减．
(2)因为y2－x2=－(x2－y2)，所以只要用分式的符号法则，即可将第2个分式的分母和另两个分式的分母化为相同的．
解：
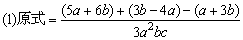
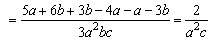
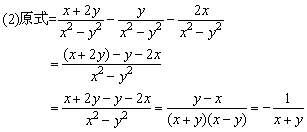
例6、计算
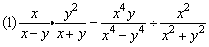
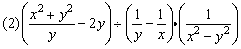
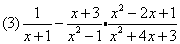
分析：
(1)先算乘除，再算加减． (2)先算括号内的． (3)先算乘法，再算减法．
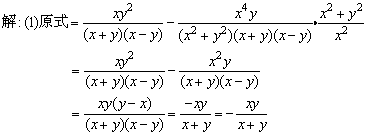
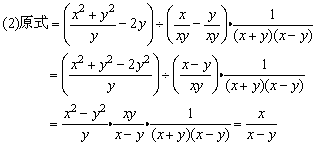
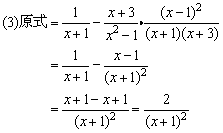
例7、化简求值：
．
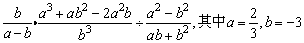分析：
本题要求先化简再求值，实际上就是先将分子、分母分别分解因式，然后约分，把分式化为最简分式以后再代入求值．
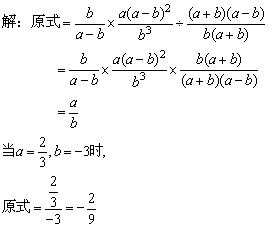
例8、计算下列各式，并把结果化为只含有正整数指数幂的形式．
(1)(a－3)－2(b2c－2)3
(2)(4x－2y3z－1)－3(8xy－2z5)2
分析：
正、负整数指数混合在一起运算，其运算顺序、运算法则类同整式、分式的运算，先做乘方、后做乘除，结果含负整数指数时，把它的指数改变符号后放在分母上或分子上．
解：
(1)(a－3)－2(b2c－2)3
=a－3×(－2)b2×3c－2×3
=a6b6c－6
=
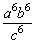
(2)(4x－2y3z－1)－3(8xy－2z5)2
=4－3x－2×(－3)y3×(－3)z－1×(－3)·82x2y－2×2z5×2
=2－6＋6x6＋2y－9＋(－4)z3＋10
=20x8y－13z13
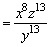
例9、计算下列各式，并把结果化为只含有正整数指数幂的形式．
(1)(a－3bc2)－2； (2)(x－3y)2·(x2y－2)2；
(3)[(－x)2(x－1)2]÷x5； (4)(2ab2)－2·(a－2)－1．
利用幂的运算性质进行计算时，计算的结果利用负整数指数幂的意义转化为正整数指数幂的形式．
解：
(1)(a－3bc2)－2=(a－3)－2·b－2·(c2)－2=a6b－2c－4=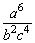
(2)(x－3y)2·(x2y－2)2=x－6·y2·x4·y－4=x－6＋4·y2＋(－4)=x－2y－2=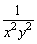
(3)[(－x)2(x－1)2]÷x5=（x2x－2）÷x5=x2＋(－2)－5=x－5=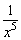
(4)(2ab2)－2·(a－2)－1=2－2a－2b－4a2=2－2·a－2＋2b－4=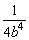
例10、将下列各数用科学记数法表示出来．
(1)某市有人口370万人．
(2)某大型计算机的计算次数已达到每秒10亿次以上．
(3)某种病毒细胞的直径为0.000 025 8毫米，约合多少米？
解：
(1)370万=370×104=3.7×102×104=3.7×106(人)
(2)10亿=10×108=1×109=109(次)
(3)0.000 025 8毫米=2.58×10－5毫米
=2.58×10－5×10－3米=2.58×10－8米
