|
一周强化
一、一周知识概述
1、反比例函数
一般地,形如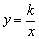 的函数(k≠0,k为常数)叫做反比例函数. 的函数(k≠0,k为常数)叫做反比例函数.
2、反比例函数的图象
反比例函数的图象是双曲线,它有两个分支,这两个分支分别位于第一、三象限或第二、四象限,它们关于原点对称,由于反比例函数中,自变量x≠0,函数y≠0,所以它的图象与x轴和y轴都没有交点,即双曲线的两个分支无限地接近坐标轴,但永远不与坐标轴相交.
3、反比例函数的图象与性质
反比例函数 |
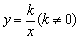
|
k的符号 |
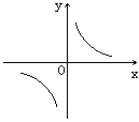
k>0 |
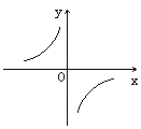
k<0 |
图象 |
|
|
性质 |
①x的取值范围是x≠0,y的取值范围是y≠0
②函数图象的两个分支分别在第一、三象限,在每一个象限内,y随x的增大而减小 |
①x的取值范围是x≠0,y的取值范围是y≠0
②函数图象的两个分支分别在第二、四象限,在每一个象限内,y随x的增大而增大 |
4、用待定系数法求反比例函数的解析式
反比例函数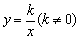 图象上的点的坐标满足函数关系式;满足函数关系式的一对x、y值对应的点在其函数图象上,因此,已知反比例函数图象上一个点的坐标,就能用待定系数法确定其解析式. 图象上的点的坐标满足函数关系式;满足函数关系式的一对x、y值对应的点在其函数图象上,因此,已知反比例函数图象上一个点的坐标,就能用待定系数法确定其解析式.
二、重点难点疑点突破
1、反比例关系与反比例函数的区别与联系
(1)小学数学中讲述当矩形的面积S一定时,矩形的长a与宽b成反比例关系,那时所说的a与b均为常数.现在我们所说的反比例函数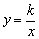 (k为非零常数),这时的x与y均为变量.但它们有一个共同的特点:ab=S,xy=k,即其积为一个常数. (k为非零常数),这时的x与y均为变量.但它们有一个共同的特点:ab=S,xy=k,即其积为一个常数.
(2)成反比例的关系式,不一定是反比例函数,如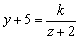 中,y+5与z+2成反比例,但y不是关于z的反比例函数;再如 中,y+5与z+2成反比例,但y不是关于z的反比例函数;再如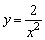 中,y与x2成反比例,但y不是关于x的反比例函数,因为这里的分母中,x的指数不是1. 中,y与x2成反比例,但y不是关于x的反比例函数,因为这里的分母中,x的指数不是1.
2、正确认识反比例函数及其形式
当常数k≠0时,xy=k或y=kx-1是反比例函数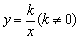 的变形形式(隐函数形式). 的变形形式(隐函数形式).
但通常写成显函数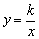 的形式.如 的形式.如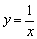 不要写成1-xy=0, 不要写成1-xy=0,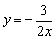 不要写成2xy+3=0. 不要写成2xy+3=0.
3、反比例函数的图象与性质
(1)反比例函数图象的位置是:当k>0时,x、y同号,图象为第一、三象限的两支曲线;当k<0时,x、y异号,图象为第二、四象限的两支曲线,故又称反比例函数为双曲线.
(2)若点(a,b)在反比例函数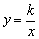 的图象上,则点(-a,-b)也在此图象上,故反比例函数的图象关于原点对称. 的图象上,则点(-a,-b)也在此图象上,故反比例函数的图象关于原点对称.
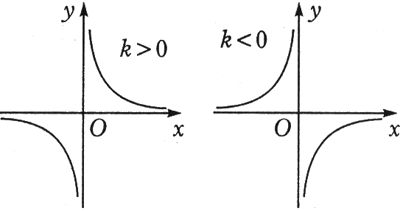
(3)对于k>0,当x取正值且越来越大时,y也取正值但越来越小,所以这时反比例函数的图象在第一象限越来越接近x轴(但不与x轴相交);当x取正值越来越小时,y也取正值但越来越大,这时其图象在第一象限内越来越接近y轴(但不与y轴相交).其图象如图(甲)所示.依对称性不难知道其图象在第三象限内的变化趋势.
对于k<0的情况,类似可得,其图象如图(乙)所示.
4、反比例函数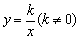 中的比例系数k的几何意义 中的比例系数k的几何意义
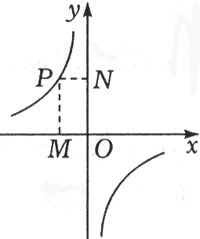
依反比例函数的表达式,我们不难得到k=xy(k≠0),如图,过双曲线上任一点P作x轴、y轴的垂线PM、PN,所得的矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=|k|.
即在反比例函数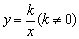 的图象上任取一点向两坐标轴作垂线,则两垂线线段与两坐标轴所围成的矩形的面积等于|k|,且这个面积的值与取点的位置无关. 的图象上任取一点向两坐标轴作垂线,则两垂线线段与两坐标轴所围成的矩形的面积等于|k|,且这个面积的值与取点的位置无关.
三、解题方法技巧点拨
1、利用反比例函数的定义确定函数解析式
例1、当m=________时,函数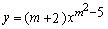 是反比例函数. 是反比例函数.
解:
∵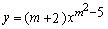 是反比例函数, 是反比例函数,
∴m2-5=-1,即m2=4,∴m=2或m=-2.
又m+2≠0,故m≠-2.
∴m=2时,y=4x-1=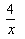 为反比例函数.故填m=2. 为反比例函数.故填m=2.
点拨:
若称y=kxn是反比例函数,则依反比例函数的定义,必须满足两个条件:①n=-1;②k≠0.两个条件缺一不可.
2、利用反比例关系解题
例2、已知y与x-1成反比例,且当x=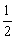 时,y= 时,y=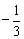 ,那么当x=2时,y的值为______. ,那么当x=2时,y的值为______.
解:
设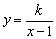 ,即k=(x-1)y(k≠0). ,即k=(x-1)y(k≠0).
将x=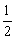 ,y= ,y=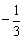 代入,得 代入,得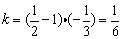 . .
∴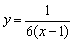 ,当x=2时, ,当x=2时,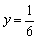 . .
点拨:
两个变量的代数式之间成反比例关系时,也涉及到先确定其反比例的系数k的问题,这一点与反比例函数极其相似.
3、用待定系数法来确定反比例函数解析式
例3、已知一次函数y=2x-k的图象与反比例函数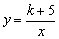 的图象相交,其中有一个交点的纵坐标为-4.求这两个函数的解析式. 的图象相交,其中有一个交点的纵坐标为-4.求这两个函数的解析式.
解:
依题意知,在这个交点处y=-4,故有
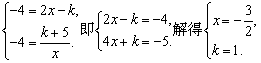
检验知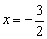 ,k=1符合题意. ,k=1符合题意.
故一次函数的解析式为y=2x-1;反比例函数的解析式为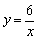 . .
点拨:
待定系数法是确定函数解析式的一种常用方法,在一次函数中我们已经学习过,跟正比例函数y=kx一样,由于反比例函数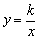 中只有一个系数k待定,通常只需知道图象过某一点就可以待定出系数k来.而本例只给出一个点的一个坐标,通过反比例函数与一次函数的交点,用联立方程组来待定k和另一坐标x,这都是待定系数法确定函数解析式的常用方法. 中只有一个系数k待定,通常只需知道图象过某一点就可以待定出系数k来.而本例只给出一个点的一个坐标,通过反比例函数与一次函数的交点,用联立方程组来待定k和另一坐标x,这都是待定系数法确定函数解析式的常用方法.
例4、如图,一次函数y=kx+b的图象和反比例函数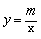 的图象相交于A、B两点. 的图象相交于A、B两点.
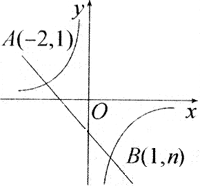
(1)利用图中条件,求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数值大于反比例函数的值的x的取值范围.
分析:
由图象知,一次函数和反比例函数的图象都经过A(-2,1)、B(1,n).可先把A(-2,1)的坐标代入反比例函数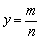 中,求出反比例函数解析式,再将 B(1,n)代入所求反比例函数解析式中,求出n的值,然后将A(-2,1)、B(1,n)的坐标分别代入一次函数解析式,求出k、b的值,也可以将A(-2,1)、B(1,n)的坐标分别代入一次函数和反比例函数解析式,列出一个方程组,然后解方程组求出待定系数的值,从而得出函数解析式. 中,求出反比例函数解析式,再将 B(1,n)代入所求反比例函数解析式中,求出n的值,然后将A(-2,1)、B(1,n)的坐标分别代入一次函数解析式,求出k、b的值,也可以将A(-2,1)、B(1,n)的坐标分别代入一次函数和反比例函数解析式,列出一个方程组,然后解方程组求出待定系数的值,从而得出函数解析式.
解:
(1)方法1:把x=-2,y=1代入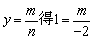 ,∴m=-2. ,∴m=-2.
∴反比例函数的解析式为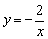 . .
把x=1,y=n代入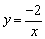 中得 中得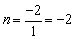 , ,
即B点坐标为(1,-2).
将点A、B坐标代入y=kx+b,得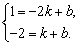
解这个方程组得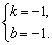
∴一次函数解析式为y=-x-1.
方法2:因为A、B两点都在双曲线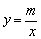 和直线y=kx+b上. 和直线y=kx+b上.
∴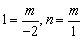 ,1=-2k+b,n=k+b, ,1=-2k+b,n=k+b,
解这个方程组得m=-2,n=-2,k=-1,b=-1.
∴反比例函数的解析式为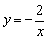 ,一次函数解析式为y=-x-1. ,一次函数解析式为y=-x-1.
(2)由图象和(1)知,反比例函数和一次函数图象的交点坐标为(-2,1),(1,-2)即x=-2或x=1时,一次函数和反比例函数值相等,当x<-2或0<x<1时一次函数值大于反比例函数的值.
4、利用反比例函数中xy为常数来解题
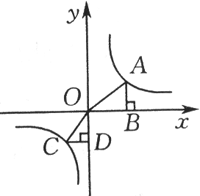
例5、如图,A、C是函数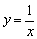 的图象上的任意两点,过A点作x轴的垂线,垂足为B;过C点作y轴的垂线,垂足为D.记Rt△AOB的面积为S1,Rt△COD的面积为S2,则() 的图象上的任意两点,过A点作x轴的垂线,垂足为B;过C点作y轴的垂线,垂足为D.记Rt△AOB的面积为S1,Rt△COD的面积为S2,则()
A.S1>S2
B.S1=S2
C.S1<S2
D.S1与S2的大小关系不能确定
解:
S1=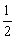 |OB|·|AB|= |OB|·|AB|=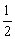 |xA|·|yA|= |xA|·|yA|=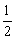 , ,
S2=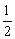 |CD|·|OD|= |CD|·|OD|=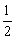 |xC|·|yC|= |xC|·|yC|=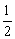 . .
∴S1=S2.故选B.
点拨:
因为点A、C在反比例函数的图象上,所以xy=1.此题是利用反比例函数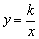 中xy=k(常数)来解题. 中xy=k(常数)来解题.
5、正、反比例函数的图象的两个交点关于原点对称
例6、已知正比例函数y=kx与反比例函数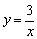 的图象都过点A(m,1),求此正比例函数的解析式及另一个交点的坐标. 的图象都过点A(m,1),求此正比例函数的解析式及另一个交点的坐标.
解:
∵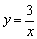 的图象过点A(m,1),∴m=3. 的图象过点A(m,1),∴m=3.
将A(3,1)坐标代入y=kx,得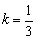 . .
∴此正比例函数的解析式为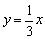 . .
∵正比例函数与反比例函数的图象都是关于原点对称的,
∴其交点也是关于原点对称的,故另一个交点的坐标是(-3,-1).
点拨:
这里指出了,因为正比例函数y=k1x的图象和反比例函数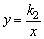 (k1k2≠0)的图象都关于原点对称,所以它们的两个交点关于原点对称. (k1k2≠0)的图象都关于原点对称,所以它们的两个交点关于原点对称.
拓展:
(1)反比例函数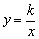 (k≠0)的图象与一次函数y=ax+b(b≠0)的图象的两个交点关于原点对称吗? (k≠0)的图象与一次函数y=ax+b(b≠0)的图象的两个交点关于原点对称吗?
(2)本例还有其他解法没有,试试看.
6、不可忽视反比例函数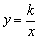 中k的符号功能 中k的符号功能
例7、已知反比例函数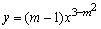 的图象在第二、四象限,则m的值为_______. 的图象在第二、四象限,则m的值为_______.
解:
∵y是反比例函数,∴3-m2=-1,即m2=4.
又∵此反比例函数的图象在第二、四象限,
∴m-1<0,即m<1.
解方程组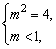 得m=-2. 得m=-2.
点拨:
对反比例函数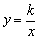 ,若其图象在第一、三象限,则x、y同号,k>0;若其图象在第二、四象限,则x、y异号,k<0,反之亦然.这就是k的符号功能. ,若其图象在第一、三象限,则x、y同号,k>0;若其图象在第二、四象限,则x、y异号,k<0,反之亦然.这就是k的符号功能.
在解有关正、反比例函数及一次函数问题时,若能做到眼中有式(函数解析式),脑中有图(函数的图象),数与形紧密结合,解题时就能灵活自如了.
例8、已知反比例函数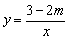 ,当x<0时,函数y随x的增大而减小,求非负整数m的值. ,当x<0时,函数y随x的增大而减小,求非负整数m的值.
分析:
因为反比例函数y随x的增大而减小,所以函数图象分布在第一、三象限,故3-2m>0.
解:
依题意得
3-2m>0,即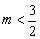 . .
又∵m为非负整数,∴m为1或0.
方法规律:描述函数的增减性,必须指出“在每一个分支(象限)内”,若在同一个象限内,则可直接比较,如果是跨象限比较时,只能根据图象进行比较,不能生搬硬套.
例9、在函数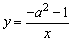 (a为常数)的图象上有三点(-3,y1),(-1,y2),(2,y3)则函数值y1,y2,y3的大小关系是() (a为常数)的图象上有三点(-3,y1),(-1,y2),(2,y3)则函数值y1,y2,y3的大小关系是()
A.y2<y3<y1 B.y3<y2<y1
C.y1<y2<y3 D.y3<y1<y2
分析:
∵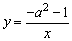 是反比例函数, 是反比例函数,
且-a2-1=-(a2+1)<0,
∴双曲线分布在第二、四象限,在各象限内,y随x的增大而增大.
∵(-3,y1)和(-1,y2)在第二象限,且-3<-1,
∴y1<y2.又∵(2,y3)在第四象限,
∴y3<y1,y3<y2.故可知它们的大小关系.
答案:D.
- 返回 -
|