一周强化

一、一周知识概述

1、正方形的定义及性质

　　有一组邻边相等并且有一个角是直角的平行四边形叫正方形．

　　从定义可知，正方形既是一种特殊的矩形（有一组邻边相等的矩形），又是一种特殊的菱形（有一个角是直角的菱形），因此它具有矩形和菱形的所有性质．

　　

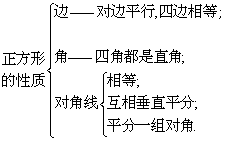
　　正方形被对角线分成的三角形，都是等腰直角三角形．

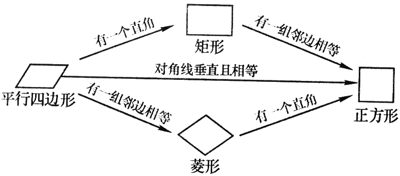
2、正方形的判定

　　从平行四边形出发：有一组邻边相等且有一个角是直角的平行四边形是正方形．

　　从矩形出发：有一组邻边相等的矩形是正方形．

　　从菱形出发：有一个角是直角的菱形是正方形．

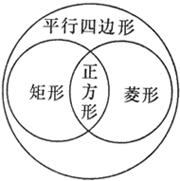
3、平行四边形、矩形、菱形、正方形的关系

　　正方形、矩形、菱形都是特殊的平行四边形，它们的包含关系如图．

二、重难点知识归纳

　　正方形的判定和性质的综合运用是重点．

　　几种特殊的平行四边形的判定的恰当选择是难点．

三、例题解析

1、利用正方形对角线的性质解题

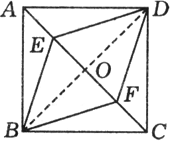
例1、如图，在正方形ABCD中，点E、F在AC上，且AE=CF．请猜测四边形BEDF的形状，并对你的猜测给出合理的说明．

解：

　　四边形BEDF为菱形．理由如下：

　　连结BD交AC于点O．

　　∵四边形ABCD为正方形，

　　∴OB=OD，OA=OC，

　　又AE=CF，∴OE=OF．

　　∴四边形BEDF是平行四边形．又∵AC⊥BD

　　∴四边形BEDF为菱形

点拨：

　　正方形的对角线互相垂直平分且相等的性质，会为解题带来很多方便．

例2、如图，正方形ABCD的对角线交于点O，E是OA上任一点，CF⊥BE于点F，CF交OB于点G．求证：OE=OG．

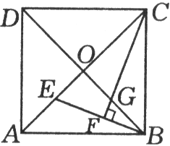
证明：

　　∵四边形ABCD为正方形，

　　∴对角线AC、BD互相垂直平分于点O，即OB=OC，OB⊥AC．

　　又CF⊥BE，∴∠BGF=∠OEB．

　　∴∠OGC=∠BGF=∠OEB．

　　∴Rt△BOE≌Rt△COG，∴OE=OG．

点拨：

　　这里主要是应用正方形对角线互相垂直平分来破题的．

2、利用正方形的轴对称性解题

例3、如图，已知E、F分别是正方形ABCD的边BC、CD上的点，AE、AF分别与对角线相交于点M、N．若∠EAF=50°，求∠CME＋∠CNF的度数．

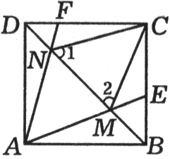
解：

　　在四边形AECF中，

　　∵∠ECF=90°，∠EAF=50°，

　　∴∠AEC＋∠AFC=360°－（90°＋50°）=220°．

　　∵NC与NA、MC与MA均关于直线BD对称，

　　∴∠MCN=∠EAF=50°，∴∠1＋∠2=130°．

　　又五边形MECFN内角和为540°，

　　∴∠CME＋∠CNF

　　=540°－(∠1＋∠2)－(∠AEC＋∠AFC)－∠ECF

　　=540°－130°－220°－90°=100°．

点拨：

　　利用正方形的对称性作角和线段的转化十分快捷，如图中∠BMA=∠BMC，∠DAN=∠DCN，AM=CM，AN=CN等．

例4、已知，如图，在正方形ABCD中，点E在AC上．

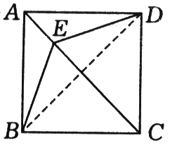
　　（1）求证：BE=DE；

　　（2）你能将上面的命题用文字概括为一个命题吗？

　　（3）你能用这个命题证明下面这道题吗？请写出证明过程．如图，点P在正方形ABCD的对角线AC上，PE⊥AB，PF⊥BC，E、F是垂足．求证：EF=PD．

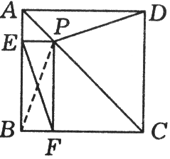
解：

　　（1）∵点E在AC上，点B、D关于AC对称，∴BE=DE．

　　（2）能用文字概括为“正方形一条对角线上的一点和另一条对角线的两端距离相等”．

　　（3）能．证明：连结BP，由（2）可知BP=DP，

　　又∵PE⊥AB，PF⊥BC，∴∠PEB=∠PFB=90°．

　　又∵∠ABC=90°，∴四边形EBFP是矩形，

　　∴BP=EF，∴EF=DP．

点拨：

　　该题（1）的结论是一个常用到的正方形的性质，也可用对称的知识或证△ABE≌△ADE得到，在例3中该图已经出现过；第（3）小题的证明思路是，抓住正方形是轴对称图形这一特点，把正方形沿对称轴AC翻折，使PD翻折到PB，把要证PD=EF转化为只要证PB=EF，从而达到把分散的条件集中到一块的目的．

3、利用旋转法解决有关正方形问题

例5、如图，正方形ABCD的边长AB=20，F为AD上一点，连结CF，作CE⊥CF交AB的延长线于点E，作DG⊥CF交CF于点G．若BE=15，求DG的长．

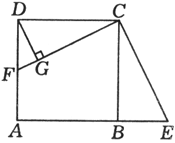
解：

　　Rt△CDF绕点C旋转90°后可以得到Rt△CBE，

　　∴Rt△CDF≌Rt△CBE．

　　∴DF=BE．

　　∴．

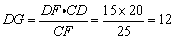点拨：

　　分析条件DC⊥CB，CF⊥CE，CD=CB，于是可以将Rt△CDF旋转，旋转实质还是两个三角形全等．

例6、如图，在一正方形花池ABCD内需要装一只喷头P，且满足PA︰PB︰PC=1︰2︰3．求∠APB的度数．

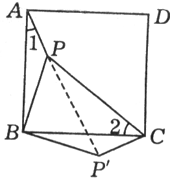
解：

　　将△APB绕B点顺时针旋转90°得△CP′B，连结PP′．

　　∵PA︰PB︰PC=1︰2︰3，

　　∴可设PA=P′C=x，PB=P′B=2x，PC=3x．

　　又△PBP′为等腰直角三角形，

　　∴PP′2=PB2＋P′B2=(2x)2＋(2x)2=8x2．

　　又PC2=(3x)2=9x2，　　∴P′C2＋P′P2=PC2．

　　∴∠PP′C=90°．

　　故∠BP′C=45°＋90°=135°．

　　∴∠APB=∠BP′C=135°．

点拨：

　　这里是通过旋转，将分散的条件集中起来，再由三角形边与边的关系，求出有关角的大小．

4、构造正方形解题

例7、如图，RA⊥AB，QB⊥AB，P是AB上一点，RP=PQ=a，RA=h，QB=k，∠RPA=75°，∠QPB=45°．求AB的长．

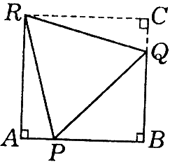
解：

　　过R作BQ的垂线交BQ延长线于点C，则AB=RC．

　　∵∠RPA=75°，∠QPB=45°，

　　∴∠RPQ=180°－(75°＋45°)=60°，

　　∠PQB=90°－45°=45°．

　　又RP=PQ，∴△PRQ是等边三角形，

　　∴RP=RQ．

　　又∠RQC=180°－(60°＋45°)=75°，

　　∴∠RQC=∠RPA，∴Rt△APR≌Rt△CQR．

　　∴AB=RC=AR=h．

点拨：

　　此题是通过补图，构造正方形求解．

5、利用正方形性质解选择题

例8、如图，有两个正方形和一个等边三角形，则图中度数为30°的角有（ ）

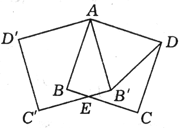
A．1个　　　　　　　　　　　　　B．2个

C．3个　　　　　　　　　　　　　D．4个

解：

　　如图．

　　∵△AB′D为正三角形，四边形ABCD、四边形AB′C′D′均为正方形，

　　∴∠BAB′=∠B′DC=30°．

　　在四边形ABEB′中，易知∠BEB′=360°－90°×2－30°=150°．

　　故∠BEC′=∠B′EC=30°．

　　故选D．

点评：

　　本题极易误选B．

- 返回 -