|
一周强化
一、一周知识概述
1、梯形的概念
梯形是指一组对边平行而另一组对边不平行的四边形,这两个条件缺一不可.换一种说法就是,一组对边平行且不相等的四边形是梯形.
等腰梯形和直角梯形是两种特殊梯形.
2、等腰梯形的性质与判定
(1)等腰梯形的性质
①等腰梯形是轴对称图形,它只有一条对称轴,底边的垂直平分线是它的对称轴;
②等腰梯形同一底边上的两个角相等;
③等腰梯形的两条对角线相等.
(2)等腰梯形的判定
同一底上两个角相等的梯形是等腰梯形.
3、梯形中常见辅助线作法
(1)平移一腰,使两腰、两底角集中于同一个三角形中,并且得出两底之差(如图(1));
(2)平移一条对角线,使两条对角线及两底之和构成一个三角形,并且能得出两底之和(如图(2));
(3)延长两腰交于一点,将梯形转化为三角形(如图(3));
(4)作梯形的高,将梯形转化为矩形与直角三角形(如图(4));
(5)延长顶点与一腰中点的连线交底边于一点,将梯形转化为三角形,并且集中了两底(如图(5));
(6)将梯形割补为平行四边形(如图(6));

二、重难点知识归纳
1、掌握梯形、等腰梯形、直角梯形等有关概念,并了解它们之间的关系.
2、探索等腰梯形的有关性质和常用判别方法,并能运用它们进行有关的证明和计算.
3、通过对梯形辅助线的探索,学会将未知问题转化为已知问题,培养化归意识.
三、典型例题剖析
1、直接利用等腰梯形的性质或判定解题
例1、如图,P为等腰梯形ABCD的下底BC上一点,PM⊥AB,PN⊥CD,M,N为垂足,BE⊥CD,E为垂足.求证:BE=PM+PN.
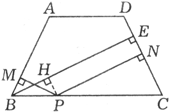
证明:
过P点作PH⊥BE于点H.
∵BE⊥CD,PN⊥CD,∴四边形PHEN是矩形.
∴HE=PN,EN∥PH.∴∠BPH=∠C.
∵四边形ABCD为等腰梯形,∴∠ABC=∠C.
∴∠MBP=∠HPB.
又PM⊥AB,BP公共,∴Rt△MBP≌Rt△HPB.∴PM=BH.
∴BE=BH+HE=PM+PN.
点拨:
要证线段的和差问题,通常可以考虑用“截长法”或“补短法”来完成,本例采用的是“截长法”.
例2、如图,已知矩形ABCD中,E、F分别是AO、DO的中点.求证:四边形BCFE是等腰梯形.
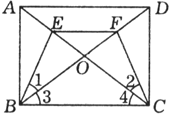
证明:
∵四边形ABCD是矩形,
∴OA=OB=OC=OD,AD∥BC.
又E、F分别是OA、OD中点,
∴EF∥AD,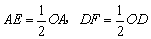 . .
∴EF∥BC.又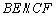 , ,
∴四边形EBCF是梯形.
又OE=OF,∴△EOB≌△FOC(SAS).∴∠1=∠2
又∠3=∠4,∴∠EBC=∠FCB
∴梯形EFCB是等腰梯形.
点拨:
这里是先根据梯形定义,判定四边形BCFE是梯形,再证同一底上两底角相等.
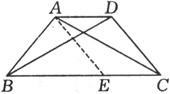
例3、如图,已知四边形ABCD中,AB=DC,AC=DB,AD≠BC.求证:四边形ABCD是等腰梯形.
证明:
过点A作AE∥DC交BC边于点E.
∵AB=CD,AC=DB,BC=CB,
∴△ABC≌△DCB,∴∠ABC=∠DCB
又AE∥DC,∴∠AEB=∠DCB
∴∠ABC=∠AEB ,∴AB=AE,∴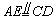 . .
∴四边形AECD是平行四边形.∴AD∥BC.
又AB=DC,且AD≠BC,
∴四边形ABCD为等腰梯形.
点拨:
判定一个任意四边形为等腰梯形,如果不能直接运用等腰梯形的判定定理,一般的方法是通过作辅助线,将此四边形分解为熟悉的多边形,此例就是通过作平行线,将四边形分解成为一个平行四边形和一个等腰三角形.
2、梯形辅助线的作法
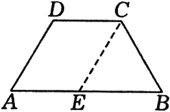
例4、如图,在等腰梯形ABCD中,DC∥AB,AB=11cm,DC=5cm,DA=6cm.求∠B的度数.
解:
过点C作CE∥DA交AB于E点,
∵DC∥AB,∴四边形AECD是平行四边形.
∴CE=DA=6cm,AE=DC=5cm.
∴EB=AB-AE=6cm,∴CE=EB
又DA=CB,∴CE=CB
∴△BCE是等边三角形.∴∠B=60°.
点拨:
过顶点作一腰的平行线,把梯形化为平行四边形和三角形,转化的目的是把条件都集中到以∠B为内角的三角形中.
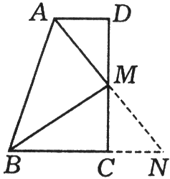
例5、如图,在梯形ABCD中,AD∥BC,且AB=AD+BC,M为DC的中点.求证:AM⊥BM.
证明:
延长AM交BC的延长线于点N.
∵M为DC中点,AD∥BC,∴△ADM≌△NCM.
∴AD=CN,AM=MN.∴AB=AD+BC=BN.
由等腰三角形“三线合一”知,BM⊥AM.
点拨:
根据证题的需要,集中梯形的两底也是常用的添加辅助线的方法.本例也可以先延长BC至N,使BN=AB,再证A、M、N共线.
例6、如图,梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=5cm,BD=12cm,求该梯形上下底的和.
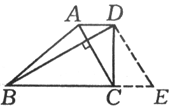
解:
过D作DE∥AC交BC的延长线于点E.
∵AD∥CE,∴DE=AC=5cm,AD=CE.
∵AC⊥BD,∴DE⊥BD.
在Rt△BDE中,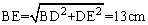
∴AD+BC=CE+BC=BE=13cm.
点拨:
过顶点作一条对角线的平行线,把两条对角线的数量关系和位置关系集中到一个三角形中,将求梯形上下底的长转化为求直角三角形斜边的长.
例7、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,且AC⊥BD,AF是梯形的高,梯形的面积是49cm2.求梯形的高.
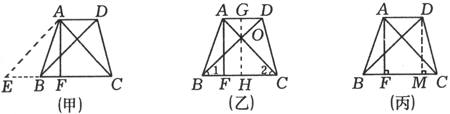
解法1:
如图(甲),过A作AE∥DB交CB的延长线于点E.
∵AC⊥BD,∴AC⊥AE.
∵AD∥EB,∴AE=BD,EB=AD.
又∵四边形ABCD是等腰梯形,∴AC=BD.∴AE=AC.
∴△AEC是等腰直角三角形.
又AF是斜边上的高,故AF也为斜边上的中线.
∴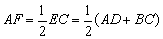
∴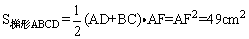
∴AF=7cm
解法2:设梯形ABCD的两条对角线相交于O点,过O作OH⊥BC于点H,延长HO交AD于G点(如图(乙)).
∵AD∥BC,∴HG⊥AD.
∵AB=DC,AC=DB,BC公共,
∴△ABC≌△DCB.∴∠2=∠1.
又∵AC⊥BD,∴△BOC是等腰直角三角形.
∴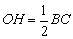 .同理 .同理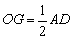 . .
∴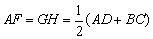 . .
以下解答过程与解法1相同.
解法3:过D作DM⊥BC于点M(如图(丙)).
∵梯形ABCD是等腰梯形,∴AC=DB,∠ABC=∠DCB.
又∵AF=DM,∴Rt△AFC≌Rt△DMB,∴∠DBC=∠ACB.
又∵AC⊥BD,∴∠DBM=∠ACF=45°.
∴△AFC和△DMB都是等腰直角三角形.∴AF=FC,DM=MB,
∴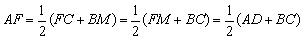 . .
以下解答过程与解法1相同.
点拨:
本题的三种解法都是利用等腰直角三角形的性质或全等三角形的性质来证明该梯形的高就等于该梯形的中位线的长.因此,在等腰梯形中,若两条对角线垂直,则这个梯形的高就等于中位线的长,梯形的面积就等于高的平方.
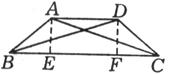
例8、如图,已知在等腰梯形ABCD中,AD∥BC.
(1)若AD=5,BC=11,梯形的高是4,求梯形的周长;
(2)若AD=a,BC=b,梯形的高是h,梯形的周长为C,则C=______;(请用含a,b,h的代数式表示;答案直接写在横线上,不要求证明)
(3)若AD=3,BC=7,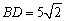 ,求证:AC⊥BD. ,求证:AC⊥BD.
解:
(1)分别过点A、D作AE⊥BC,DF⊥BC,垂足分别为E、F,则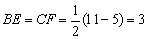 . .
又AE=DF=4,∴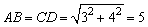
∴梯形的周长为5+11+2×5=26.
(2)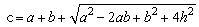 . .
(3)过点D作DG∥AC,交BC的延长线于点G.
∵AD∥BG,∴四边形ACGD是平行四边形.
∴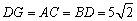 . .
而BG=BC+CG=BC+AD=7+3=10,
∵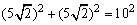 ,∴BD2+DG2=BG2. ,∴BD2+DG2=BG2.
∴BD⊥DG.∴BD⊥AC.
点评:
(1)是作等腰梯形的两条高,构造直角三角形,运用勾股定理求腰长;由(3)知在等腰梯形中,已知对角线互相垂直或要证对角线互相垂直,一般的方法就是平移一腰.
- 返回 -
|