矩形的性质定理、判定定理及菱形的性质及判定定理

同步教学

一、一周知识概述

　　本周主要学习、讨论了两种特殊的平行四边形，即矩形与菱形，并探索了它们各自独有的基本特征与性质．矩形和菱形是最为常见的平行四边形，它们既是轴对称图，又是中心对称图形．通过学习我们必须掌握好它们所具有的性质与其判定方法．

1、矩形

　　有一个角是直角的平行四边形是矩形．

2、矩形的性质定理及推论

　　性质定理①：矩形的四个角都是直角．

　　性质定理②：矩形的对角线相等．

　　推论：直角三角形斜对上的中线等于斜边的一半

3、矩形的判定定理

　　判定定理①：有三个角是直角的四边形是矩形．

　　判定定理②：对角线相等的平行四边形是矩形．

4、菱形的性质定理．

　　（1）菱形的四条边都相等．

　　（2）菱形的对角线互相垂直平分，一条对角线平分一组对角．

5、菱形的判定定理

　　（1）四条边都相等的四边形是菱形；

　　（2）对角线互相垂直的平行四边形是菱形．

二、重点知识归纳及讲解

1、矩形的性质定理．

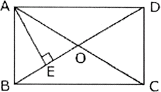
　　例1：在矩形ABCD中，AE⊥BD，∠BAE︰∠EAD=2︰3，求∠CAE的度数．

［解析与解答］

2、矩形的判定定理

　　例2：证明：平行四边形各内角平分线若围成一个四边形，则这个四边形一定是矩形．

［解析与证明］

3、菱形的性质定理

　　菱形具有平行四边形的一切性质，它还具有一般的平行四边形所不具有的性质，可分别从边和对角线的两个角度来记．

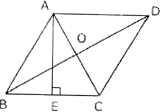
　　例3：在菱形ABCD中，AB=AC，AE⊥BC于E，求∠ADO的度数．

［解析与解答］

4、菱形的判定定理

　　判定一个四边形为菱形可以从以下三个方面着手：

　　（1）定义：有一组邻边相等的平行四边形是菱形

　　（2）判定定理1：四条边都相等的四边形是菱形

　　（3）判定定理2：对角线互相垂直平分的四边形是菱形

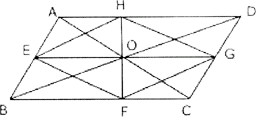
　　例4：已知平行四边形ABCD，AC、BD交于点O，EG⊥FH于O，且E、F、G、H分别在AB、
　　　　 BC、CD、DA上，求证：四边形EFGH为菱形．

［解析与解答］

三、难点知识剖析

1、中心对称和中心对称图形的联系与区别．

　　（1）联系：如果把成中心对称的两个图形看作一个图形，则这个图形为中心对称图形；如果把中心对称图形对称的部分看成两个图形，那么它们成中心对称．

　　（2）区别：中心对称是指两个全等图形之间的相互位置关系，中心对称图形是指具有特殊性质的图形．

2、中心对称和轴对称的比较

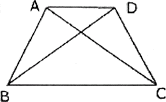
3、矩形的对角线相等，那么对角线相等的四边形一定是矩形吗？不一定，例如：

　　四边形ABCD中，AB=CD，∠BAD=∠ADC，AD<BC，可证：△ABD≌DCA，即得CA=BD，但四边形ABCD不是矩形．

- 返回 -