正方形和梯形

同步教学

一、一周知识概述

1、正方形

（1）概念：有一对邻边相等，有一个角为直角的平行四边形是正方形.

（2）性质：

①正方形的四条边都相等；

②正方形的四个角都为直角；

③正方形的对角线相等且互相垂直平分，对角线平分一组对角。

（3）判定：既是菱形又是矩形的四边形是正方形。

2、梯形：一组对边平行，另一组对边不平行的四边形。

梯形的底：梯形中平行的两边叫做梯形的底。

梯形的腰：梯形中不平行的两边叫做梯形的腰。

梯形的高：梯形两底的距离叫做梯形的高。

3、等腰梯形的性质定理

（1）等腰梯形的两腰相等，两底互相平行；

（2）等腰梯形在同一底上的两个角相等；

（3）等腰梯形的对角线相等.

4、等腰梯形的判定定理

（1）两腰相等的梯形是等腰梯形；

（2）在同一底上的两个角相等的梯形是等腰梯形；

（3）对角线相等的梯形是等腰梯形。

二、重点知识归纳讲解

　　正方形是一种更为特殊的平行四边形，它既具有平行四边形的一般性质，又具有矩形与菱形的独特性质。

　　在学习中要注意理解平行四边形、矩形、菱形和正方形各种图形之间的关系。

　　梯形经常通过划分成一个平行四边形与一个三角形来解决有关问题，通过练习，我们要深刻理解和掌握这一化归思想。

　　通过学习要认识等腰梯形的轴对称特征及其他性质。

1、正方形的性质的运用

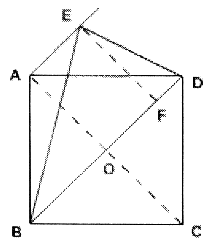
例 1、在正方形ABCD中，AE∥BD，BD=BE，求∠DBE的度数.

[解析]

2、正方形的判定

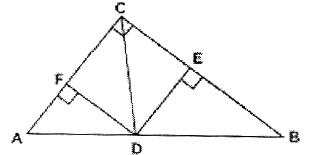
例 2、已知在△ABC中，∠C=90°，CD是角平分线，DE⊥BC，DF⊥AC.求证：四边形CFDE为正方形.

[解析]

3、在解与梯形相关的问题时，常将梯形转化为三角形和四边形.

例 3、已知等腰梯形的锐角等于60°，它的两底分别为15cm，49cm，求它的腰长.

[解析]

4、通过平移变换表示两条线段的和与差

例 4、在梯形ABCD中，AD∥BC，E、F分别为AD、BC的中点，且

∠ B＋∠C=90°，求：EF︰（BC－AD）的值.

[解析]

三、难点知识剖析

1、四边形的分类

（1）按四边形的角来分类：四边形可分为凸四边形和凹四边形；

（2）按四边形互相平行的对边的组数来分类：

两组对边都不平行：一般四边形

一组对边平行，另一组对边不平行：梯形

两组对边都平行：平行四边形

 

- 返回 -