1 、为了把多项式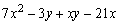
用分组分解法分解因式，正确的分组方法是（ ）
A．(7x2+xy)+(21x+3y) B．(7x2-3y)+(xy-21x)
C．(7x2-21x)+(3y-xy) D．(7x2-21x)+(xy-3y)
2 、为了把多项式 x3-x2+x-1 用分组分解法分解因式，不同的分组方法有（ ）
A．1 种 B．2 种
C．3 种 D．4 种
3 、当a 、b 取不相等的正数时，a3+b3 与a2b+ab2 的值的大小关系是（ ）
A．a3+b3=a2b+ab2 B．a3+b3﹥a2b+ab2
C．a3+b3﹤a2b+ab2 D．不能确定
4 、若 a+b+c=0，则 a3+a2c-abc+b2c+b3 的值为（）
A．-1 B．0
C．1 D．2
5 、关于多项式 x2-y2-z2+2yz+x+y-z 正确的结论是（ ）
A．不能分解因式 B．有（x-y+z+1）的因式
C．有（x+y-z+1）的因式 D．有（x-y-z+1）的因式
6 、多项式 a2-b2+2bc-c2 可分解为（ ）
A．(a+2b-c)(a+b+c) B．(a-b-c)(a-b+c)
C．(a+b-c)(a-b+c) D．(a+b-c)(-a+b-c)
7 、代数式 (x+y-2xy)(x+y-2)+(xy-1)2 可分解为（ ）
A．(x+1)2(y+1)2 B．(x-1)2(y+1)2
C．(x-1)2(y-1)2 D．(x2+1)(y+1)2
8 、为分解因式 x3+x2y-xy2-y3 分组方法如下（ ）
（1） (x3+x2y)+(-xy2-y3) （2） (x3-y3)+(x2y-xy2)
（3） (x3-xy2)+(x2y -y3) （4） (x3+x2y-xy2)-y3
其中正确的分组方法有（ ）
A．1 个 B．2 个
C．3 个 D．4 个
9 、下列各式的因式分解：
① -2x2-2y2=-2(x+y)(x-y)
② -8xy-4x2-4y2=-4(x+y)2
③ 9x2(a-b)+12xy(b-a)+4y2(a-b)=(a-b)(3x+2y)2
④ 4x2+2x+1=(2x+1)2
其中错误的是（ ）
A．只有① B．只有④
C．①和④ D．①③④
10 、若 2x3-x2-13x+k 分解因式后有一个因式 x+1 ，则 k 的值为（ ）
A．10 B．-10
C．12 D．不能确定