 |
|||
|
|
旋转与中心对称
同步教学
一、一周知识概述
本周复习第11章中的第2节与第3节的内容,即旋转与中心对称。
通过学习应明确:
1、旋转是图形的一种基本变换,而在这一章里主要研究平面图形。探索平面图形的旋转变换,了解旋转既可表示物体(图形)运动的过程,也可表示物体(图形)运动后最终的位置与原先位置的关系。体验感受图形旋转的主要因素是旋转中心和旋转的角度,从而理解在旋转过程中,图形中的每一点都绕着旋转中心转动了相同的角度,对应线段相等,对应角相等,图形的形状与大小都没有变化。
2、理解中心对称图形是旋转角度为180°的较为特殊的旋转图形,认识中心对称与中心对称图形。了解两个图形关于某一点成中心对称的本质就是其中的一个图形可以看作为另一个图形绕该点旋转180°而成,关于中心的对称点就是旋转中所说的对应点,中心对称是旋转角度为180°的较为特殊的旋转对称及中心对称的基本性质。
二、重难点知识的归纳与剖析
(一)、旋转
1、旋转的定义:
一个物体,绕某一点,由一个位置转到另一个位置,像这样的运动,就叫做旋转(rotation).
这一点叫做物体的旋转中心(centerofrotation).
2、旋转的组成:
图形的旋转是由旋转中心和旋转的角度所决定的.
3、旋转的特征:
(1)图形在旋转时,图形中每一点都绕中心旋转了同样大小的角度。
(2)图形在旋转时,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的大小和形状都没有发生改变。
4、旋转对称图形的定义:
一个图形,绕旋转中心旋转一定角度后能与它自身重合,这种图形叫做旋转对称图形(afigureofrotationsymmetry).
5、图形的旋转与旋转对称图形的区别与联系:
(1)图形的旋转是指一个图形从一个位置旋转到另一个位置,是指同一图形在位置上的变化,而旋转对称图形,是指一个图形所具有的特性,即旋转一定角度后位置没有变化,仍与自身重合。
(2)图形的旋转随着旋转角度的不同从一个位置旋转到不同的位置,而旋转对称图形旋转一定角度后仍在原处与自身重合。
(3)图形的旋转与旋转对称图形都是绕中心旋转。
6、轴对称与旋转的联系:
将一个图形连续进行两次翻折(两条对称轴相交),所得到的图形可以看作由原来的图形,经过一次旋转得到的,旋转中心是两条对称轴交点,旋转角是两条对称轴夹角的二倍。
7、旋转的性质:
一个图形从一个位置旋转到另一个位置,旋转前后图形的大小和形状不变。
重点:旋转的性质和特征。
难点:掌握两个基本要素,即旋转中心和旋转角度,判断一个图形是不是由另一个图形通过旋转产生的,要看这两个图形旋转后能否重合。
考点:通过图形的旋转证题。
(二)、中心对称
1、中心对称的定义:
把一个图形绕着某一个点旋转180°,如果它能与另一个图形重合,就说这两个图形关于这个点对称。这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
2、中心对称图形的定义:
把一个图形绕它的某一点旋转180°,如果旋转后的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形(afigureofcentralsymmetry)。这个中心点叫做对称中心(centerofsymmetry)。
3、区别与联系:
中心对称和中心对称图形是两个既有联系又有区别的概念,它们的区别是:中心对称指两个完全一样的图形间的相互位置关系,中心对称图形是指一个图形本身两部分之间的关系;它们的联系是;如果将中心对称的两个图形看成一个整体,则它们是中心对称图形,一个中心对称图形,如果把对称的部分看成两个图形,则它们是关于中心对称。
4、中心对称与轴对称之间的不同处:
5、中心对称和轴对称的联系:
如果一个轴对称图形有两条互相垂直的对称轴,那么它必是中心对称图形,这两条对称轴的交点就是它的对称中心。反之,中心对称图形不一定是轴对称图形。
6、几种特殊四边形的对称性
(1)平行四边形是以它对角线的交点为对称中心的中心对称图形;
(2)矩形、菱形、正方形不仅是中心对称图形而且是轴对称图形;
(3)矩形、菱形有两条互相垂直的对称轴;
(4)正方形的对称轴分为两组,每组有互相垂直的对称轴;
(5)等腰梯形有一条对称轴。
7、关于中心对称的两个图形的特征和识别:
特征1:关于中心对称的两个图形能完全重合。
特征2:关于中心对称的两个图形,对称点的连线都经过对称中心,并且被对称中心平分。
识别:如果两个图形的对应点连成的线段都经过某一点,并且被平分,那么这两个图形一定关于这一点成中心对称。
重点:中心对称和中心对称图形的定义及中心对称图形的特征。
难点:中心对称和中心对称图形之间的区别与联系。
考点:知道哪些图形是中心对称图形,会画一个图形关于某一点的中心对称图形。
三、例题分析
例1、在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是16,求DP的长.
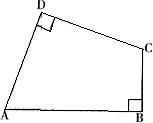
[解析]
例2、如图△ABC绕顶点C旋转某一个角度后得到△A'B'C,请问:
①旋转中心是什么?旋转角是什么?
②经过旋转,点A、B分别移动到什么位置.
③找出图中所有相等的角和相等的线段.
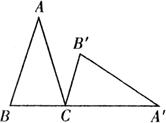
[解析]
例3、如图,按要求画一个图形:所画图形中同时要有正方形和圆,并且这个图形既是中心对称图形又是轴对称图形。
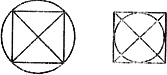
[解析]
例4、如图所示的两个图形是不是轴对称图形?如果是,请画出对称轴.这两个图形能不能经过旋转与自身重合?如果能,分别需要旋转多少度?
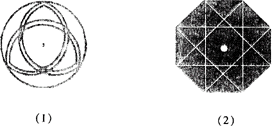
[解析]
- 返回 -
