一周强化

一、一周知识概述

1、平方根和算术平方根

　　如果一个数的平方等于 a，那么这个数叫做a的平方根（square root），即如果x2=a，则x叫做a的平方根，记作x=±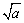，其中a叫被开方数.

　　一般地，如果一个正数x的平方等于a，即x2=a，那么这个正数x叫做a的算术平方根.

　　a的算术平方根记为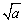，读作“根号a”，a叫被开方数.

　　0的算术平方根是0.

2、平方根的性质

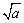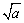　　（1）任何一个正数的平方根有两个，它们互为相反数.如正数a的平方根是±，其中＋与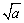－恰是一对相反数；

　　（2）零的平方根是零，即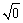=0；

　　（3）负数没有平方根.

3、平方根的表示

正数a的算术平方根用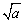表示；

正数a的负的平方根用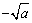表示；

正数a的平方根用符号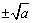表示.

4、开平方

求一个非负数的平方根的运算，叫做开平方，开平方与平方互为逆运算 .

5、平方根重要性质：

（1）a≥0时，；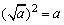

（2）.

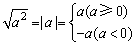6、用计算器求一个数的算术平方根

　　有的计算器上有“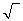”键，就可以使用这个键直接求出一个数的算术平方根.

二、重难点知识归纳

1、由算术平方根的定义得到：一个非负数a的算术平方根可记作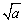，它是非负数，就是说，当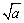有意义时，它一定表示一个非负数，故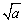具有双重非负性：①a≥0；②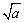≥0.

2、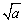是算术平方根的专有记号，它有两重意义：①表示求根号内的非负数的算术平方根，是运算符号；②求a的算术平方根，其思维方式与乘方是逆向的，即要这样想，什么非负数的平方等于a.

3、求一个数的平方根，实质上是已知指数和幂，求底数.这种求底数的运算是乘方运算的一种逆运算.

4、因为只要一个数的平方等于a，那以这个数的相反数的平方也一定等于a，所以正数a有两个平方根.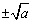

5、弄清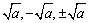的意义：

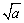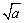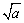（1）弄清（a≥0）表示非负数，即≥0，表示a的算术平方根；

（2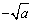）（a≥0）表示a的算术平方根的相反数，也可以说是表示a的负的平方根；

（3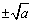）（a≥0）表示a的平方根，即a的平方根为.

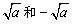6、用计算器求一个数的算术平方根，如果被开方数不是完全平方数，如果所求得的算术平方根是它的近似值，此时应根据题目的要求进行四舍五入．根据计算器的类型，掌握不同的按键顺序.

7、平方根与算术平方根的区别及联系

　　区别：

　　（1）定义不同：“如果一个数的平方等于a，这个数就叫做a的平方根”；“非负数a的非负平方根叫做a的算术平方根”.

　　（2）个数不同：一个正数有两个平方根，而一个正数的算术平方根只有一个.

　　（3）表示方法不同：正数a的平方根表示为±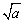，正数a的算术平方根表示为.

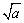　　（4）取值范围不同：正数的算术平方根一定是正数；正数的平方根则一正一负，两数互为相反数.

联系：

　　（1）具有包含关系：平方根包含算术平方根，算术平方根是平方根中的一种。

　　（2）存在条件相同：平方根和算术平方根都只有非负数才有。

　　（3）0的平方根、算术平方根均为0.

三、典型例题剖析

例1、求下列各式的值.

[解析]

例2、（1）已知，求的值；

（2）已知a、b为实数，，求a－b的平方根.

[解析]

例3、已知△ABC的三边长分别为a，b，c，且a，b满足，求c的取值范围．

[解析]

例4、小颖想用一块面积为4dm2的纸片，沿着边的方向裁出一块面积为3dm2的长方形纸片，使它的长宽之比为3︰2，你能否裁出来.

[解析]

例5、已知，求x的个位数字.

[解析]

例6、已知：.

（1）求的值；

（2）若，求x的值；

（3）若，求a的值.

[解析]

- 返回 -