1、立方根
如果一个数的立方等于 a，那么这个数叫做a的立方根（cube root），即如果x3=a，则x叫做a的立方根，记作：x=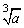
.
2、立方根的性质
①正数有一个正的立方根，负数有一个负的立方根，0的立方根是0.即a>0时，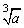
>0；a=0时，
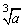=0；a<0时，
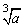<0.
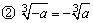，因此，求负数的立方根，可以转化为求其相反数的立方根.
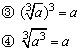
⑤若一个数的小数点向左（或向右）移动3n位，则它的立方根的小数点向左（或向右）移动n位.
3、开立方
求一个数的立方根的运算叫做开立方.开立方与立方互为逆运算.
4、用计算器求一个数的算术平方根或立方根
有的计算器上有“
”键和“
”，就可以使用这个键直接求出一个数的算术平方根或立方根.
5、实数的概念及其分类
（1）定义：有理数和无理数统称为实数.
（2）实数的分类：
①按定义分类
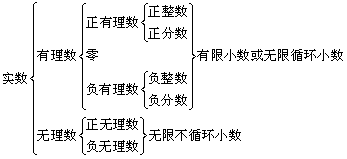
②按大小分类
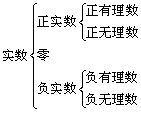
6、实数和数轴上点的对应关系
实数和数轴上的点是一一对应的关系，即数轴上的每一个点都表示一个实数，反过来，每个实数都可以在数轴上找到表示它的点.
实数大小的比较
一切正数都大于零；一切负数都小于零；一切正数大于一切负数；两个负数比较，绝对值大的反而小.即
绝对值大的负数＜绝对值小的负数＜零＜正数.
在数轴上表示的两个实数，右边的数总比左边的数大.
1、立方根与平方根的联系及区别
两者联系：
（1）都与相应的乘方运算互为逆运算。开平方与平方互为逆运算，开立方与立方互为逆运算.
（2）在研究被开方数和方根的关系时，都有类似小数点的移动规律.
（3）零的立方根和平方根都是它本身.
两者区别：
（1）在用符号表示平方根时，根指数2可省略，而用符号表示立方根时，根指数3不能省略.
（2）只有非负数才有平方根，而任何数都有立方根.
（3）正数的平方根有两个，而正数的立方根只有一个.
（4）被开方数的小数点移动两位时，平方根的小数点向相同方向移动一位；被开方数的小数点移动三位时，立方根的小数点向相同方向移动一位.
2、无限不循环小数叫做无理数，包括以下几类：
（1）开方开不尽的数，如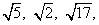
…；
（2）有特定意义的数，如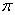
及含
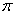的数；
（3）无限不循环小数，如0.808008000…等．
无理数的特征：
（1）无理数的小数部分位数不限；
（2）无理数的小数部分不循环，不能表示成分数的形式．
3、实数中的几个概念
（1）相反数：a与－a互为相反数，0的相反数是0.
注意：两个相反数之和等于0.
（2）倒数：若a≠0，则a与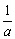
互为倒数.
说明：两个互为倒数的数之积等于1.
（3）绝对值：正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0，即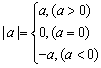
4、实数与数轴上的点一一对应
（1）每一个实数都可以用数轴上的点来表示；
（2）数轴上的每一个点都表示一个实数.
5、实数大小的比较
一切正数都大于零；一切负数都小于零；一切正数大于一切负数；两个负数比较，绝对值大的反而小.即
绝对值大的负数＜绝对值小的负数＜零＜正数.
在数轴上表示的两个实数，右边的数总比左边的数大.
6、用计算器求一个正数的平方根或求立方根时，应注意精确度，或根据精确度取近似数.
7、实数的运算
在实数范围内可以进行加、减、乘、除（0不能作除数）、乘方运算；正数和0可以进行开任意次方（如开平方、开立方等）运算，负数不能开偶次方（如负数不能开平方）运算.
注意：
（1）无理数不都是带根号的数，如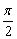
，0.3030030003….
（2）带根号的数不都是无理数，只有那些开不尽的方根属于无理数，开得尽的方根是有理数.如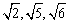
等是无理数，而
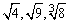等是有理数.
（3）关于有理数的运算律和运算性质在实数范围内仍然成立，但要注意正数和零可以进行开平方、开立方运算，但负数能开立方运算，却不能开平方运算.
；（2）
.
是3b－6a－3的立方根，
，且x＋y=0，求x
； （4）(3x＋0.1)
.
化成分数的形式．