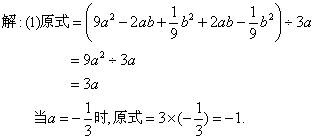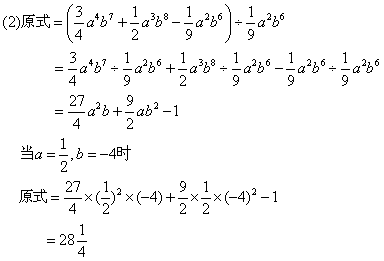一周强化

一、一周知识概述

1、单项式除以单项式

　　单项式相除，把系数与同底数幂分别相除作为商的因式.对于只在被除式里含有的字母，则连同它的指数作为商的一个因式.

2、多项式除以单项式

　　多项式除以单项式，先把这个多项式的每一项除以这个单项式，再把所得的商相加.

3、整式乘除法的比较

　　跟整式的乘法一样，整式的除法关键是掌握好同底数幂的除法和单项式与单项式相除．为此，不妨将二者进行归纳、比较．

运算	同底数幂	单项式
相乘	底数不变， 指数相加	把它们的系数、相同字母分别相乘，对只在一个单项式里含有的字母，则连同它的指数作为积的一个因式
相除	底数不变， 指数相减	把系数与同底数幂分别相除作为商的因式，对只在被除式里含有的字母，则连同它的指数作为商的一个因式

二、重难点知识归纳

　　以同底数幂的除法，幂的运算法则的综合应用以及单项式除以单项式，多项式除以单项式为重点.

　　以整式的综合运算为难点.

三、典型例题剖析

例1、计算：

(1)(xy)m＋n＋1÷(xmyn·xny)；

(2)(－2a3b2c)2·(－4a2b3)3÷(－4a5b4c)2．

分析：

　　依运算顺序先乘方，再作乘除运算．单项式除以单项式的顺序为：①系数相除；②相同字母相除；③被除式中单独有的字母，连同它的指数一起作为商的一个因式．(2)中，先作乘方运算后，因乘除是同级运算，故一次性按同底数幂的运算法则处理，就会使运算简便、直观．

解：

　　(1)原式=xm＋n＋1ym＋n＋1÷(xm＋nyn＋1)

　　　　　 =x(m＋n＋1)－(m＋n)y(m＋n＋1)－(n＋1)=xym；

　　(2)原式=(4a6b4c2)·(－43a6b9)÷(42a10b8c2)

　　　　　 =－41＋3－2a6＋6－10b4＋9－8c2－2

　　　　　 =－42a2b5c0=－16a2b5．

例2、计算：

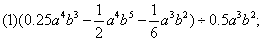
(2))(a2m＋1b3－3am＋2b4－5amb5)÷(－amb3)；

(3)[2(a＋b)5－3(a＋b)4＋(－a－b)3]÷[2(a＋b)3].

分析：

　　(1)（2）题应先利用法则把多项式除以单项式的运算转化为单项式除以单项式运算，进而求出最后结果，(2)题应注意符号；（3）题应运用整体思想把a＋b看成是一个字母，按多项式除以单项式的法则计算.作多项式除以单项式的运算时，除了要认真细致，不漏项、不串项外，还要特别防止因符号而出现错误．

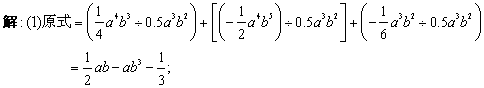
　　(2) 原式=a2m＋1b3÷(－amb3)－3am＋2b4÷(－amb3)－5amb5÷(－amb3)

　　　　　　=－am＋1＋3a2b＋5b2=－am＋1＋3a2b＋5b2；

　　(3)原式

　　　=[2(a＋b)5÷2(a＋b)3]＋[－3(a＋b)4÷2(a＋b)3]＋[－(a＋b)3÷2(a＋b)3]

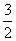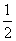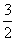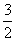　　　=(a＋b)2－(a＋b)－=a2＋2ab＋b2－a－b－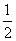

例3、完成下列各题：

(1)已知xm=8，xn=5，求xm－n的值；

(2)已知xm=a，xn=b，求x2m－3n的值；

(3)已知3m=6，9n=2，求32m－4n＋1的值.

分析：

　　运用幂的有关性质将结论中的代数式转化为含有已知条件的代数式，即可求值.

解：

　　(1)∵xm=8，xn=5，

　　∴xm－n= xm÷xn=8÷5=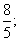

(2)∵xm=a，xn=b

　　∴x2m－3n= x2m÷x3n=(xm)2÷(xn)3=a2÷b3=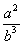

(3)∵3m=6，9n=32n=2

　　∴32m－4n＋1=(3m)2÷(32n)2×3

　　　=62÷22×3

　　　=36×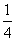×3=27

例4、化简求值：

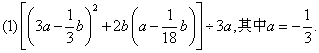
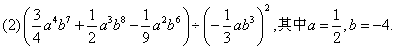
分析：

　　第(1)题中应先将中括号内化简，再运用法则计算；第(2)题先化简除式，再运用法则计算.

　　

- 返回 -