1、因式分解的意义
把一个多项式化成为几个整式的积的形式，叫做多项式的因式分解.
总结：(1)因式分解是多项式的一种恒等变形，也是单项式与多项式，多项式与多项式相乘的逆变形.
(2)分解因式是对多项式而言的，且分解的结果必须是整式的积的形式.
(3)分解因式都是在指定的数集内进行(如无特殊说明，一般指有理数)，其结果要使每一个因式不能再分解为止.
2、提公因式法
(1)公因式：多项式中每一项都含有的因式，叫公因式.
(2)提公因式法：如果一个多项式的各项含有公因式，那么就可以把这个公因式提出来，从而将多项式化成几个因式乘积的形式，这种分解因式的方法叫做提公因式法.
(3)公因式的构成：
①系数：各项系数的最大公约数；
②字母：各项都含有相同字母；
③指数：相同字母的最低次幂.
提公因式时要一次提尽.
3、公式法
（1）平方差公式
把整式乘法的平方差公式(a＋b)(a－b)=a2－b2，反过来就得到：
a2－b2=(a＋b)(a－b)
即两个数的平方差，等于这两个数的和与这两个数的差的积.
（2）完全平方公式
把整式乘法的完全平方公式
(a±b)2=a2±2ab＋b2
反过来，就得到a2±2ab＋b2=(a±b)2
即两个数的平方和加上(或减去)这两个数的积的2倍，等于这两个数的和(或差)的平方.
4、分解因式的步骤可归纳为“一提二公三检查”.
“一提”是一开始可考虑各项是否都有公因式，即是分解因式的第一个步骤也是第一个方法。
“二公”即在提取了公因式后，根据具体情况看剩下的多项式是二项多项式或是三项多项式，若是两项多项式，可考虑是否能用“平方差公式”分解因式；若是三项多项式可考虑是否能用“完全平方公式”，将这个多项式分解到不能再分解为止。
“三检查”是指分解因式后检查结果是否正确，要分解到不能再分解为止．
1、正确理解因式分解的含义
“把一个多项式化成几个整式的积的形式叫做多项式的因式分解”，也叫做把这个多项式分解因式．”对这段文字的理解应注意如下几点：
(1)“分解因式”与“因式分解”是同义语；
(2)
，即因式分解为整式乘法的逆向变形；
(3)应从整体上把握因式分解的含义，如
m2＋8m－9=(m2－9)＋8m=(m＋3)(m－3)＋8m就不是因式分解，
而m2＋8m－9=(m＋9)(m－1)才符合因式分解的要求．
2、怎样提取公因式
提公因式法是因式分解最基本也是最常用的方法，它的关键是确定公因式，难点是提取公因式后括号内多项式的确定．
(1)公因式的系数为各项系数的最大公约数，相同字母的最低次数．
如8x3y2－6x2y3＋2xy4的公因式为2xy2；
(2)提取公因式后括号内的多项式的项数与原多项式的项数相同，各项恰为原多项式的各项分别除以公因式所得的商．
如8x3y2－6x2y2＋2xy4=2xy2(4x2－3x＋y2)．
3、分解因式必须分解到每个因式在有理数范围内不能再分解为止
如 a4－1=(a2＋1)(a2－1)不正确，因为a2－1还可以继续分解为(a+1)(a－1)，即
a4－1=(a2+1)(a+1)(a－1)
4、对某些多项式还要了解经过一定变形后才能分解的因式，如：分解x2－4xy＋3y2的因式，此题用现有的方法还不能分解因式.但若适当处理后配成完全平方，就可以继续分解.
x2－4xy＋3y2=x2－4xy＋3y2＋y2－y2=x2－4xy＋4y2－y2
=(x－2y)2－y2=(x－2y＋y)(x－2y－y)
=(x－y)(x－3y)
例1、（1）下列各式中从左到右的变形，是因式分解的是（ ）
A．(x＋5)(x－5)=x2－25 B．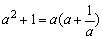
C．x2y－xy2=xy(x－y) D．15=3×5
（2）下列各式的因式分解中正确的是（ ）
A．－a2＋ab－ac=－a(a＋b－c)
B．9xyz－6x2y2=3xyz(3－2xy)
C．3a2x－6bx＋3x=3x(a2－2b)
D．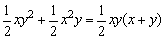
解析：
（1）显然，A是乘法运算，不正确；B分解因式是将多项式分成几个整式的积，而右边有分式；D是常数，是单项式，不是多项式，不属于分解因式范围，所以C是正确的.
（2）A．提－a后括号里面各项要变号，但第二、三项未变号.
B．第二项没有公因式z.
C．提3x后，括号里第三项还有因数1，掉了一项.
D．是正确的.
答案：（1）C；（2）D
例2、把下列各式分解因式：
(1)6x4y2－12x3y＋27x2y3； (2)－x4y＋x3y2－x2y3；
(3)xn＋3xn－1＋xn－2； (4)5(x－y)3＋10(y－x)2；
(5)m(5ax＋ay－1)－m(3ax－ay－1).
分析：
分解因式时，首先要看多项式各项有无公因式，若有公因式，应先提取公因式，要对数字系数和字母分别进行考虑，如果系数为整数，应该提各项系数的最大公约数；字母考虑两点：一点是取各项相同的字母，一点是各项相同字母的指数取最低的；公因式提出后，剩下的因式的求法是：用公因式去除多项式的每一项，所得的商即为剩下的因式.
一个多项式中的公因式，既可以是一个单项式，也可以是一个多项式，注意用整体思想去观察分析多项式，关于幂的底数的符号与指数有如下规律：
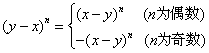
解：
(1) 6x4y2－12x3y＋27x2y3
=3x2y·2x2y－3x2y·4x＋3x2y·9y2=3x2y(2x2y－4x＋9y2)
(2)－x4y＋x3y2－x2y3=－(x4y－x3y2＋x2y3)
=－(x2y·x2－x2y·xy＋x2y·y2)
=－x2y(x2－xy＋y2)
(3)xn＋3xn－1＋xn－2=xn－2·x2＋xn－2·3x＋xn－2·1
=xn－2(x2＋3x＋1)
(4)5(x－y)3＋10(y－x)2=5(x－y)3＋10(x－y)2
=5(x－y)2(x－y＋2)
(5)m(5ax＋ay－1)－m(3ax－ay－1)
=m[(5ax＋ay－1)－(3ax－ay－1)]
=m·(5ax＋ay－1－3ax＋ay＋1)
=m(2ax＋2ay)=2ma(x＋y)
例3、把下列各式分解因式：
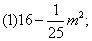(2)(a＋b)2－1；(3)－(x＋2)2＋16(x－1)2；
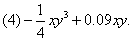
分析：
运用平方差公式分解因式，其关键在于对公式的识别和把要分解的多项式“对号入座”.首先应考虑有无公因式可提，其次，“找”相当于公式中的字母a，b，往往是以多项式或单项式形式出现的，我们应将其看做一个“整体”来替换公式中的字母a，b，从而套用公式分解因式.(1)中把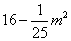
写成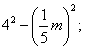
(2)把1看成12，可利用平方差公式分解；(3)先用交换律改写成16(x－1)2－(x＋2)2再改写成[4(x－1)]2－(x＋2)2；(4)先提公因式－xy，得另一个因式为
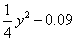再将其分解因式.
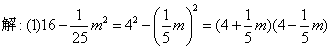
(2)(a＋b)2－1=(a＋b＋1)(a＋b－1)
(3)－(x＋2)2＋16(x－1)2=[4(x－1)]2－(x＋2)2
=[4(x－1)＋(x＋2)][4(x－1)－(x＋2)]
=(5x－2)(3x－6)=3(5x－2)(x－2)
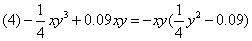
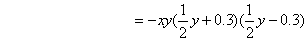
例4、把下列各式分解因式：
(1)x2＋14x＋49; (2)(m＋n)2－6(m＋n)＋9;
(3)－3ax2＋6axy－3ay2; (4)(x2＋4)2＋8x(x2＋4)＋16x2.
(5)64m2n2－(m2＋16n2)2; (6)(x＋y)2＋4(x－y)2－4(x2－y2).
分析：
运用完全平方公式分解因式，关键是确定符合公式的a、b这两个数(或式)，同时注意提公因式法的运用.(5)题有两项，符号相反，可以考虑用平方差公式，分解成[8mn＋(m2＋16n2)][8mn－(m2＋16n2)],再套用完全平方公式分解;(6)题有两个平方项(x＋y)2,[2(x－y)]2，而另一项－4(x2－y2)=－2(x＋y)·2(x－y)也符合公式特点.
解：(1)x2＋14x＋49=x2＋2·x·7＋72=(x＋7)2
(2)(m＋n)2－6(m＋n)＋9=(m＋n－3)2
(3)－3ax2＋6axy－3ay2=－3a(x2－2xy＋y2) =－3a(x－y)2
(4)(x2＋4)2＋8x(x2＋4)＋16x2
=(x2＋4)2＋2·(x2＋4)·4x ＋(4x)2
=(x2＋4＋4x)2
=(x＋2)4
(5)64m2n2－(m2＋16n2)2
=(8mn)2－(m2＋16n2)2
=(8mn＋m2＋16n2)(8mn－m2－16n2)
=(m＋4n)2[－(m－4n)2]
=－(m＋4n)2(m－4n)2
(6)(x＋y)2＋4(x－y)2－4(x2－y2)
=(x＋y)2－2(x＋y)·2(x－y)＋[2(x－y)]2
=[x＋y－2(x－y)]2
=(x＋y－2x＋2y)2
=(3y－x)2
例5、（1）已知x3＋x2＋x＋1=0，求1＋x＋x2＋x3＋x4＋…＋x2003的值.
（2）已知x3＋x2y＋xy2＋y3=5，x2＋y2=10，求x＋y的值.
（3）求证a(a＋1)(a＋2)(a＋3)＋1是一个完全平方式.
解析：
（1）这个多项式共有 2004 项，由已知： 1＋x＋x2＋x3=0.
可推出多项式前四项之和为零，从第五项到第八项：
x4＋x5＋x6＋x7=x4(1＋x＋x2＋x3)=0 ，……
最后四项是 x2000(1＋x＋x2＋x3)=0.
∴ 2004 项可分为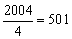
组，每组的和均为零，其值为零 .
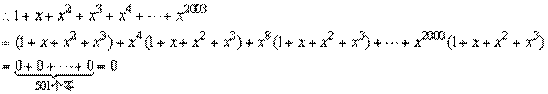
（2）∵ x3＋x2y＋xy2＋y3=5 ，∴ x2(x＋y)＋y2(x＋y)=5.
即 (x＋y)(x2＋y2)=5 ，把 x2＋y2=10 代入得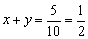
.
（3）将 a(a＋1)(a＋2)(a＋3) 的积中分成两大项，使其与 1 共三项，
然后可构成完全平方式，这就要用到先退一步，然后再进一步，即先做乘法再分解因式，将 a(a＋1)(a＋2)(a＋3) 相乘时，因式要恰当搭配。
a(a＋1)(a＋2)(a＋3)＋1=[a(a＋3)][(a＋1)(a＋2)]＋1
=(a2＋3a)(a2＋3a＋2)＋1=(a2＋3a)[(a2＋3a)＋2]＋1
=(a2＋3a)2＋2(a2＋3a)＋1=[(a2＋3a)＋1]2=(a2＋3a＋1)2.
∴ a(a＋1)(a＋2)(a＋3)＋1 可化为 (a2＋3a＋1) 的完全平方形式，
由以上式子可以得出“四个连续整数的积与 1 的和是一个整数的平方”，
请按上面方法你能计算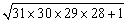
吗？（结果为869）．
例6、某超市共有四层，第一层有商品(a＋b)2种，第二层有商品a(a＋b)种，第三层有商品(a＋b)b种，第四层有商品(a＋b)3种，当a=8，b=12时，求超市商品共有多少种.
解析：
先把四层楼商品种数相加可利用分解因式.
∵(a＋b)2＋a(a＋b)＋(a＋b)b＋(a＋b)3
=(a＋b)2[1＋(a＋b)]＋(a＋b)(a＋b)
=(a＋b)2(a＋b＋1)＋(a＋b)2
=(a＋b)2(a＋b＋1＋1)
=(a＋b)2(a＋b＋2)
（先把1，4项；2，3项分别提公因式，简便）
把a=8，b=12代入计算.
∴(a＋b)2(a＋b＋2)=(8＋12)2(8＋12＋2)=202×22=400×22=8800.
即这种超市共有8800种商品供顾客选择。
