1、平行四边形的性质
平行四边形的性质较多,按“边、角、对角线”分类去研究易于理解和应用.
(1)边:平行四边形对边平行、对边相等;
(2)角:平行四边形对角相等,邻角互补;
(3)对角线:平行四边形的对角线互相平分.
对角线是将四边形转化为三角形的桥梁,平行四边形中也常利用“对角线互相平分”这一性质解决问题.
(4)平行四边形是中心对称图形,它的对称中心是两条对角线的交点.
2、平行四边形的判定方法
平行四边形判定方法除它的定义外,还有如下几种方法:
(1) 一组对边平行且相等的四边形是平行四边形;
(2) 两组对边分别相等的四边形是平行四边形;
(3)两条对角线互相平分的四边形是平行四边形.
判定一个四边形是平行四边形需两个条件,这两个条件必须对应,若已知一组对边平行,可证另一组对边平行或这组对边相等;若已知一组对边相等,可证这组对边平行或另一组对边相等;若已知一条对角线被一点平分,则需证另一条对角线也被此点平分.但要注意一组对边平行,另一组对边相等的四边形不一定是平行四边形.
特别说明的是:平行四边形的定义既是它的性质,又是它的判定.
例1、下列命题:
①一组对边平行,另一组对边相等的四边形是平行四边形;
②对角线平分的四边形是平行四边形;
③在四边形ABCD中,AB=AD,BC=DC,那么这个四边形ABCD是平行四边形;
④一组对边相等,一组对角也相等的四边形是平行四边形.
其中正确命题的个数是( )
A.0个 B.1个 C.3个 D.4个
分析:
能够由定义、公理、定理推得的命题是真命题,要说明一个命题是假命题只要举出一个反例说明它不成立即可.对于(1)等腰梯形符合条件但不是平行四边形;对于(2)“对角线平分”不够准确,没有说明两条对角线怎样平分,应为“对角线互相平分”;对于(3)不是两组对边相等,而是两邻边分别相等,不能判断是平行四边形;对于(4),如图,△ABC是等腰三角形,AB=AC,在△ADE与△DAC中,DE=AC,∠ACD=∠AED,所以AB=DE,∠AED=∠B,符合条件,但四边形ABDE不是平行四边形.
解:A
误区警示:注意区分平行四边形性质和判定的条件和结论,可从“边、角、对角线”三个方面去理解和掌握平行四边形的性质和判定.
例2、如图,在□ABCD中,EF∥AB,GH∥AD,图中有多少个平行四边形?
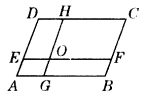
分析:用平行四边形的定义来判断.
解:
在□ABCD中,∵EF∥AB,GH∥AD,
∴EF∥AB∥CD,GH∥AD∥BC.
∴除□ABCD外,还有□AGOE、□AGHD、□ABFE、□GBFO、□GBCH、 □FCHO、 □FCDE、 □HDEO,即图中有9个平行四边形.
点评:平行四边形的定义是判定一个四边形是不是平行四边形的方法之一.
例4、如图,在□ABCD中,点E、F在BD上,且BF=DE,
(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H,请补全图形,证明四边形AGCH是平行四边形.
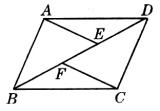
分析:
(1)利用平行四边形的性质;(2)欲证明四边形AGCH是平行四边形,已知AH//CG,故需证明AG//CH,或证明AH=CG即可证之.
解:
(1)△ABE≌△CDF,△AED≌△CFB,△ABD≌△CDB;
(2)补全图形如图,
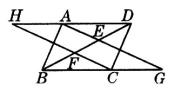
∵BF=DE,∴ BF+FE=DE+EF,即BE=DF.
∵四边形ABCD是平行四边形,
∴AB//CD.∴∠ABD=∠CDB.
在△ABE和△CDF中: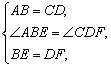
∴△ABE≌△CDF,∴∠AEB=∠CFD,
∴HC//AG,
∴四边形AGCH为平行四边形.
反思:
证明一个四边形是平行四边形选择适当的判定方法是关键,本题(2)是运用平行四边形的定义来证明的,你能运用AH与CG平行且相等证明吗?
例4、(1)有四边形ABCD和下列条件:①AB∥CD;②AD∥BC;③AB=CD;④AD=BC.从上面4个条件中选出两个,能说明四边形ABCD是平行四边形的有________;
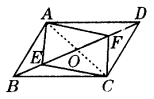
(2)如图,BD是□ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需要增加的一个条件是________(填上你认为正确的一个即可).
分析:
(1)首先确定共有六种选法:①②,①③,①④,②③,②④,③④,然后根据判定方法选出正确的结论.
(2)研究补充条件后,只要能证明四边形AECF有两组对边分别平行(或两组对边分别相等,或一组对边平行且相等,或对角线互相平分)即可.如图,若添加条件BE=DF,连接AC交BD于O,因为四边形ABCD是平行四边形,所以AO=CO,BO=DO,所以BO-BE=DO-DF,即OE=OF.所以四边形AECF是平行四边形.
解:
(1)①②为定义;①③,②④为一组对边平行且相等;①④,②③为一组对边平行,另一组对边相等,可能是等腰梯形故排除;③④为两组对边分别相等.综上所述有:符合的是①②,①③,②④,③④,共四种方法.
(2)BE=DF或BF=DE或AE∥FC等
点评:
(2)题是一道与平行四边形判定有关的题设开放型题目,关键要理解平行四边形的判定方法.
例6、如图,在△ABC中,∠ACB=90°,CF是斜边上的高,AT平分∠CAB交CF于点D,过D作DE∥AB交BC于点E.求证:CT=EB.