例1、已知代数式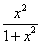
，当x分别为
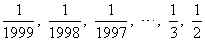，1，2，3，4，5，……1997，1998，1999时，求所给的代数式值的和.
解析：
x的取值共有2×1999－1个，其中有1998对的值互为倒数，只有x=1时只1个，这就是x取值规律，可先将一对值对应的代数式化简，再求值.
解：
（1）当x=a和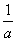
时，（1≤a≤1999，a为整数），代数式的值的和是：
.
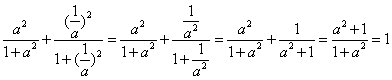即这1998对的值中的每一对的值的和为1，这是一个妙算.
（2）当x=1时，代数式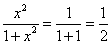
.
∴所求代数式的值的总和为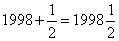
.
例2、甲、乙两工人生产同一种零件，甲每小时比乙每小时多生产8个，现在要求甲生产出168个这种零件，要求乙生产出144个零件，他们两个人谁能先完成任务呢？
分析：
理解题意，找准关系是解决数学应用题的一大规律．本例应设出甲或乙每小时生产零件的个数，计算他们各自需要的时间，由时间差的符号判断谁需要的时间少，即谁先完成任务．
解：
设乙每小时生产这种零件x个，则甲每小时生产零件(x＋8)个，甲完成任务需要时间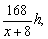
乙完成任务需要时间
．
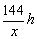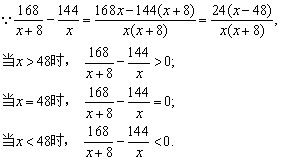
所以如果乙每小时生产零件多于48个，则乙先完成任务，如果乙每小时恰好生产48个零件，则两人同时完成任务，如果乙每小时生产零件小于48个，则甲先完成任务．
