例、一小船由A港到B港顺流需要6小时，由B港到A港逆流需要8小时，一天，小船从早晨6点由A港出发顺流到B港时，发现一救生圈掉落在水中，立刻返回，一小时后找到救生圈，问：
（1）若小船按水流速度从A港漂流到B港需要多少小时？
（2）救生圈是在何时掉入水中的？
解析：
这是一道流水问题，有顺水速度=静水速度＋水流速度，逆水速度=静水速度－水流速度。
解：
（1）设小船由A港漂流到B港需要x小时，两港距离为1.
∴水流速度是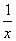
，依题意，得
．
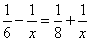解得x=48（小时），经检验符合题意.
答：小船按水流速度从A港到B港漂流需要48小时．
（2）设救生圈在x点钟落入水中，由（1），水流速度是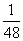
.
当小船到达B港时，正是6＋6=12（点），再返回，依题意
．
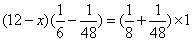解此方程：12－x=1，∴x=11（时）
答：救生圈在上午11时落入水中．
另解：设救生圈在x点钟落入水中，小船返回找到救生圈时已是13时了，这时救生圈在水中流了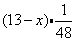
的距离，应等于小船在救生圈落水后所走的距离，减去返回距离，所以
．
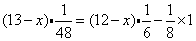解此方程7x=77，∴x=11．
