A 卷
开始测试
B 卷
二、填空题
9、内角和为1080°的多边形是__________边形.
10、若正多边形一个内角是144°,则它是_________边形.
11、已知过m边形的一个顶点有7条对角线,n边形没有对角线,k边形共有k 条对角线,则(m-k)n=_____________.
12、用边长都相等的正三角形、正方形、正六边形铺满地面(你选择一种正多边形或二种正多边形),其方案有_______种,分别是________________.
13、某足球场需铺设草皮,现有正三角形、正五边形、正六边形、正八边形、正十边形5种形状的草皮,请你帮助工人师傅选择两种草皮来铺设足球场,可供选择的两种组合是____________________.
14、一个八边形,如果它的每个内角都相等,那么它的内角等于________.
15、若一个n边形的边数增加一倍,则内角和将__________________.
[答案] 三、解答题
16、有两个各内角都相等的多边形,它们的边数之比为1∶2,且第二个多边形的内角比第一个多边形的内角大15°,求这两个多边形的边数.
[答案]
17、某同学计算多边形内角和时,得到的答案是1340°,老师指出他把某一个外角也加了进去. 你能知道这个同学计算的是几边形的内角和?而他多加的那个外角是多少度呢?
[答案]
18、如图,求图中∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数之和.
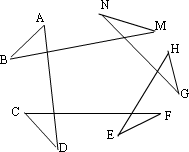
[答案]
19、一个多边形木板在不影响其他角的大小情况下,截去一个角,得到的新多边形木板的内角和是3240°,求原多边形的内角和.
[答案]
20、我们常用各种多边形地砖砌成美丽的图案,也就是说,使用给定的某些多边形,能够拼成一个平面图形,既不留一丝空白,又不互相重叠,这在几何里叫做平面密铺(镶嵌),我们知道,当围绕一点拼在一起的几个多边形的内角的和为360°时,就能够拼成一个平面图形.某校研究性学习小组研究平面密铺的问题,其中在探究用两种边长相等的正多形边形做平面密铺的情形时用了以下方法:
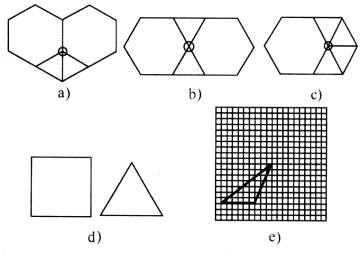
如果用x个正三角形、y个正六边形进行平面密铺,可得60°·x+120°·y=360°,化简得x+2y=6.因为x、y都是正整数,所以只有当x=2,y=2或x=4,y=1时上式才成立,即2个正三角形和2个正六边形或4个正三角形和1个正六边形可以拼成一个无缝隙、不重叠的平面图形,如图a、b、c所示.
(1)请你仿照上面的方法研究用边长相等的x个正三角形和y个正方形进行平面密铺的情形,并按图d中给出的正方形和正三角形的大小大致画出密铺后图形的示意图(只要画出一种图形即可);
(2)如果用形状、大小相同的如图e方格纸中的三角形,能进行平面密铺吗?若能,请在方格纸中画出密铺的设计图.
[答案] |