例1、(常州)如图,已知∠1=∠2,P为BN上一点,且PD⊥BC于D,AB+BC=2BD,求证:∠BAP+∠BCP=180°.
分析:要证明两个角的和是180°,可把它们移到一起,证它们是邻补角即可,由PD⊥BC,∠1=∠2,联想到过P作BA的垂线PE,有PE=PD,BE=BD,又由AB+BC=2BD得AE=CD,故△APE≌△CPD,从而有∠EAP=∠PCB,故问题得证:
由AB+BC=2BD得BC-BD=BD-AB,即CD=BD-BA,故可以在BD上截取BF=BA.
证法一:过P作PE⊥BA于E,如图所示,
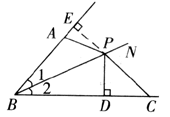
∵PD⊥BC,∠1=∠2
∴PE=PD(角平分线上一点到角的两边距离相等)
在Rt△BPE和Rt△BPD中
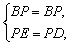 ∴Rt△BPE≌Rt△BPD. ∴Rt△BPE≌Rt△BPD.
∴BE=BD.
∵AB+BC=2BD,BC=CD+BD,AB=BE-AE,
∴AE=CD
∵PE⊥BE,PD⊥BC,∴∠PEB=∠PDC=90°
在△PEA和△PDC中
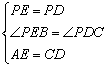 ,∴△PEA≌△PDC. ,∴△PEA≌△PDC.
∴∠PCB=∠PAE
∵∠BAP+∠EAP=180°
∴∠BAP+∠BCP=180°.
证法二:在BC上截取BF=BA,连接PF,如图所示.
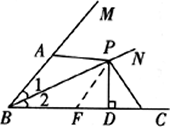
∵AB+BC=2BD
即BC-BD=BD-AB
∵BF=BA
∴BC-BD=BD-BF
∴CD=FD.
在△PDF和△PDC中
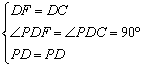 , ,
∴△PDF≌△PDC
∴∠PCB=∠PFD
在△BAP和△BFP中
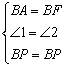 , ,
∴△ABP≌△FBP
∴∠BAP=∠BFP
∵∠BFP+∠PFC=180°
∴∠BAP+∠PCB=180°
证法3:如图所示,延长BC到E,使DE=BD,连接PE,
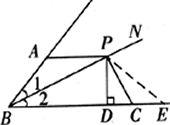
∵PD⊥BD
∴∠BDP=∠EDP=90°
在△BDP和△EDP中
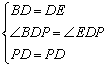
∴△BDP≌△EDP
∴BP=PE,∠2=∠PEC
又∵∠1=∠2 ,∴∠PEC=∠1
∵AB+BC=2BD,DE=BD
∴AB=CE
在△ABP和△CEP中
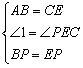
∴△ABP≌△CEP
∴∠BAP=∠ECP
又∵∠BCP+∠ECP=180°,
∴∠BCP+∠BAP=180°.
|