|
主讲:方敏文
一周强化
一、一周知识概述
1、二次根式的乘法法则
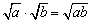 (a≥0,b≥0) (a≥0,b≥0)
即:两个二次根式相乘,把被开方数相乘,根指数不变.
注意:①此法则可推广到多个二次根式的情况:如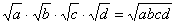 (a,b,c,d都是非负数); (a,b,c,d都是非负数);
②如果根号前有系数,就把各个系数相乘,仍旧作为二次根号前的系数;
③二次根式运算的结果,应该尽量化简,如最终结果不要写成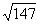 ; ;
④被开方数相乘的时候,往往不求出乘积,而是考虑因数分解或因式分解,以便进一步的化简. 如 直接得到 直接得到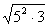 ,而不要先写成 ,而不要先写成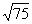 ; ;
⑤二次根式相乘也要有一定的灵活性,如果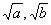 不是最简二次根式,也可以先把它们化简成最简二次根式,然后再相乘,反而简便些. 如 不是最简二次根式,也可以先把它们化简成最简二次根式,然后再相乘,反而简便些. 如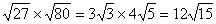 . .
2、二次根式的除法法则
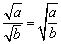 (a≥0,b>0) (a≥0,b>0)
即两个二次根式相除,把被开方数相除,根指数不变.
注意:①如果根号前有系数,就把各个系数相除,仍旧作为二次根号前的系数;
②这种方法的局限性比较大,它只适用于被除式与除式的被开方数恰好能整除的情况. 如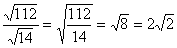 . 当被除式与除式的被开方数不能整除时,如 . 当被除式与除式的被开方数不能整除时,如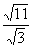 我们把它化成 我们把它化成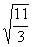 没有什么意义,这时就要采用分母有理化的方法来进行. 因此二次根式的除法运算,通常是采用化去分母中根号的方法来进行. 没有什么意义,这时就要采用分母有理化的方法来进行. 因此二次根式的除法运算,通常是采用化去分母中根号的方法来进行.
③二次根式相除,最后的结果必须化成最简二次根式.
3、二次根式的混合运算
二次根式的混合运算顺序与有理数中的运算顺序一样,先乘方,再乘除,最后加减,有括号的先算括号里的(或先去掉括号).
注意:①在运算过程中,每一个根式可以看作是一个“单项式”,多个被开方数不同的二次根式的和可以看作“多项式”;
②有理数(或整式)中的运算律、运算法则及所有的乘法公式在二次根式的运算中仍然适用;
③二次根式的运算结果必须是最简二次根式.
二、重难点知识
1、注意逆用二次根式的乘除法则,即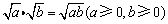 , ,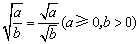 ,利用这两个性质可以对二次根式进行化简. ,利用这两个性质可以对二次根式进行化简.
2、二次根式的运算中,最后结果中的二次根式要化为最简二次根式或整式.最简二次根式必须满足两个条件:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.
3、二次根式的混合运算顺序与实数的运算顺序一样,先乘方开方,再乘除,最后加减,有括号的先算括号里的(或先去掉括号).在运算过程中,每个根式可以看作是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”;实数运算中的运算律(分配律、结合律、交换律)、运算法则及所有的乘法公式(平方差公式、完全平方公式等),在二次根式的运算中仍然适用.
三、典型例题讲解
例1、计算
(1)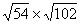 ; ;
(2)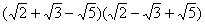 ; ;
(3)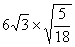 . .
分析:
逆向利用积的算术平方根的性质,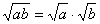 (a≥0,b≥0)得到 (a≥0,b≥0)得到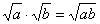 (a≥0,b≥0)这就是二次根式的乘法法则. 有理数的运算律、乘法公式对于二次根式同样适用. (a≥0,b≥0)这就是二次根式的乘法法则. 有理数的运算律、乘法公式对于二次根式同样适用.
解:
(1)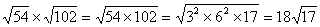
(2)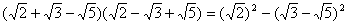
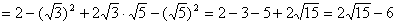
(3)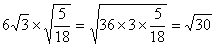
例2、计算
(1)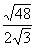 ;(2) ;(2) ;(3) ;(3)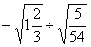 ;(4) ;(4) ; ;
(5)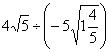 ;(6) ;(6)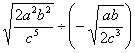 . .
分析:
利用二次根式除法法则进行,被开方数相除时,用除以一个数(非零)等于乘以这个数的倒数,约分再化简.
解:
(1)原式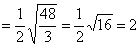 . .
(2)原式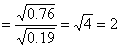 . .
(3)原式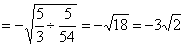 . .
(4)原式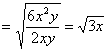 . .
(5)原式 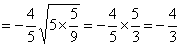 . .
(6)原式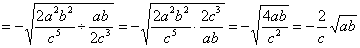 . .
小结:
当除式是分数或分式时,可转化为乘法计算.运算的结果一定要最简.即:①被开方数不能有开得尽方的因数或因式;②被开方数中不能含有分母.
例3、有一种房梁的截面积是一个矩形,且矩形的长与宽之比为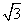 ∶1,现用直径为3 ∶1,现用直径为3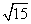 cm的一种圆木做原料加工这种房梁,那么加工后的房染的最大截面积是多少? cm的一种圆木做原料加工这种房梁,那么加工后的房染的最大截面积是多少?
解:设矩形房梁的截面宽为x(cm),则长为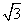 xcm,依题意, xcm,依题意,
得:(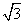 x)2+x2=(3 x)2+x2=(3 )2, )2,
4x2=9×15,x=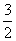 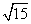 (cm), (cm),
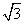 x·x= x·x=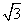 x2= x2=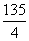 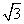 (cm2). (cm2).
例4、计算下列各题
(1)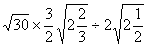
(2)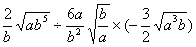
分析:
这是二次根式乘除的混合运算,与有理数的混合运算一样,按先后从左到右顺序进行.
解:
(1)原式=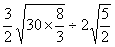
=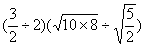
=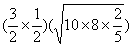
=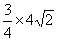
=
(2)原式=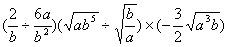
=
=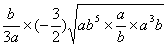
=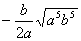
=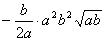
=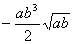
例5、计算
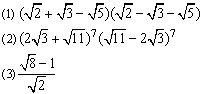
分析:
(1)可类比多项式乘法进行计算;(2)逆用幂的运算法则,能用乘法公式则宜用乘法公式计算;(3)是二次根式的除法,可按分式的基本性质计算.
解:
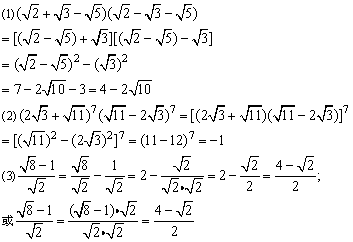
点拨:
二次根式的乘法尽量使用乘法公式,使计算简便,除法中的除式不只一项的,宜用分数(式)的基本性质,分子、分母同时乘以一个因式,使分母中的根号化去 .
例6、观察下列各式及其验证过程:
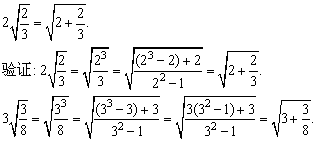
(1)按照上述两个等式及其验证过程的基本思路,猜想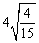 的变形结果并进行验证; 的变形结果并进行验证;
(2)针对上述各式反映的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并证明它成立.
思路:
(1)我们从两个特例入手,可以发现式子的结构特点:根号前面的数字因数和被开方数的分子相同,而分母等于分子的平方减1,于是易猜想出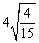 的变形结果,并得到一般规律; 的变形结果,并得到一般规律;
(2)由题设及(1)的验证结果,可猜想对任意自然数n(n≥2)都有: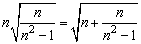 . .
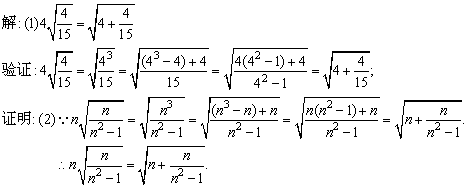
总结:
(1)本题的结论没有明确给了,需要我们去寻求和发现,合理运用猜想,就能较快地找到结论或结果,解这类题目,通常先从特殊入手,分析归纳得到一般的结果;
(2)要学会类比思想,找出规律性的东西,这是现在中考中的创新题型;
(3)在本题的规律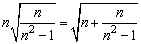 中等式右边中切忌写成 中等式右边中切忌写成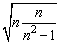 . .
- 返回 -
|