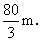例1、(新疆)如图是用硬纸板做成的四个全等的直角三角形,两直角边长分别是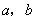 ,斜边长为c和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形.
,斜边长为c和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图.
(2)证明勾股定理.
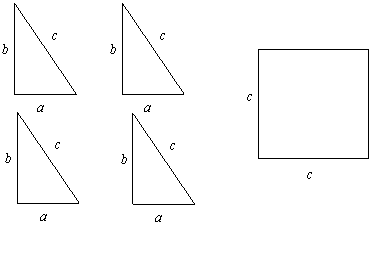
解析:
方法一、(1)如图①
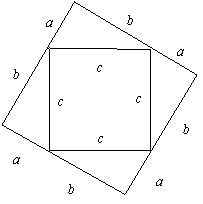
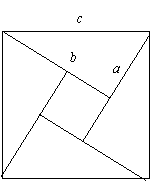
① ②
(2)证明: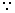 大正方形的面积表示为
大正方形的面积表示为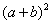 ,
,
大正方形的面积也可表示为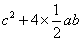 ,
,
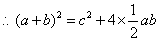 ,
,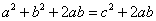 ,
,
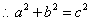 .即直角三角形两直角边的平方和等于斜边的平方.
.即直角三角形两直角边的平方和等于斜边的平方.
方法二、(1)如图②
(2)证明: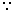 大正方形的面积表示为:
大正方形的面积表示为: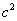 ,
,
又可以表示为: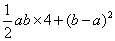 ,
,
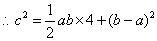 ,
,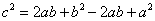 ,
,
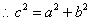 .即直角三角形两直角边的平方和等于斜边的平方.
.即直角三角形两直角边的平方和等于斜边的平方.
例2、(牡丹江)有一块直角三角形的绿地,量得两直角边长分别为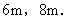 现在要将绿地扩充成等腰三角形,且扩充部分是以
现在要将绿地扩充成等腰三角形,且扩充部分是以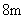 为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
解析:
在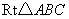 中,
中,
由勾股定理有: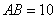 ,扩充部分为
,扩充部分为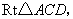 扩充成等腰
扩充成等腰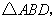 应分以下三种情况.
应分以下三种情况.
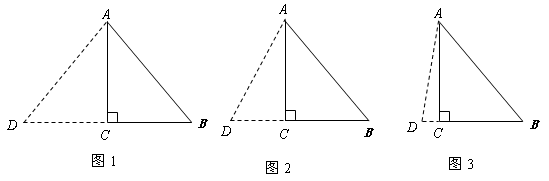
①如图1,当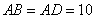 时,可求
时,可求
得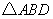 的周长为32m.
的周长为32m.
②如图2,当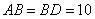 时,可求
时,可求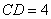
由勾股定理得: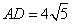 ,得
,得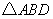 的周长为
的周长为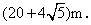
③如图3,当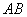 为底时,设
为底时,设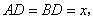 则
则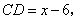
由勾股定理得: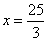 ,得
,得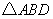 的周长为
的周长为