例、如图，直线y=－x＋2与x轴、y轴分别交于点A和点B，另一直线y=kx＋b（k≠0）经过点C（1，0），且把△AOB分成两部分.
（1）若△AOB被分成的两部分面积相等，求k和b的值；
（2）若△AOB被分成的两部分的面积比为1︰5，求k和b的值.
解：
（1）由题意得A（2，0），B（0，2）.
∵ C是OA的中点，∴ S△OBC=S△CBA.
则直线 y=kx＋b，经过C（1，0）和B（0，2）两点.
∴
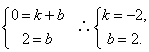
（2）设y=kx＋b与OB交于点M（0，n），且分△AOB面积为1︰5得
.
∴
．
经过点 M作MN∥OA交AB于N（a，
），则S△OMC=S△CAN.
∵ N（a，
）在直线y=－x＋2上.
∴
=－a＋2，∴ a=
.
∴ N（
，
）.
故直线 y=kx＋b经过M（0，
），C（1，0）或经过N（
，
），C（1，0）.
代入直线式，分别解得
或
.
