1、如果b>0,c>0那么二次函数y=ax2+bx+c的图象大致是( )
A.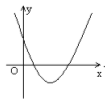 B.
B.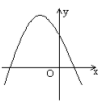
C.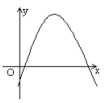 D.
D.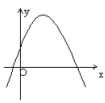
2、一次函数y=2x-3与二次函数y=x2-2x+1的图象有( )
A.一个交点 B.两个交点
C.无数个交点 D.无交点
3、已知二次函数y=mx2-2x-3的图象与x轴有交点,则m的取值范围是( )
A.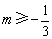 B.
B.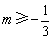
C.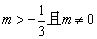 D.
D.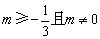
4、如果对于任意实数x,函数y=ax2+bx+c的值都是负数,那么有( )
A.a>0,b2-4ac>0 B.a<0,b2-4ac<0
C.a>0,b2-4ac<0 D.a<0,b2-4ac>0
5、如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C(0,c),∠OBC=45°,则下列各式成立的是( )