一、选择题

1、已知⊙O是△ABC的外接圆，AB=8cm，点O到AB的距离为3cm，那么⊙O的直径是（　）

A．6cm　　　　　　　　　　　　　　　　　B．8cm

C．10cm　　　　　　　　　　　　　　　　 D．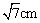

2、用反证法证明命题“若⊙O的半径为r，点P到圆心的距离为d，且d＞r，则点P在⊙O的外部”，首先应假设（　）

A．d＜r　　　　　　　　　　　　　　　　 B．d=r

C．点P在⊙O 外　　　　　　　　　　　　　D．点P在⊙O上或点P在⊙O内

3、平面直角坐标系中有点A(3,4)，以A为圆心，5为半径画圆，在同一直角坐标系中，直线y=－x与⊙A的位置关系是（　）

A．相离　　　　　　　　　　　　　　　　 B．相切

C．相交　　　　　　　　　　　　　　　　 D．以上都有可能

4、等腰△ABC的腰AB=AC=4cm，若以A为圆心，2cm长为半径的圆与BC相切，则∠BAC的度数为（　）

A．30°　　　　　　　　　　　　　　　　 B．60°

C．90°　　　　　　　　　　　　　　　　 D．120°

5、如图，AB为⊙O的直径，BC是⊙O的切线，AC交⊙O于D，AB=6，BC=8，则BD的长为（　）

A．4　　　　　　　　　　　　　　　　　　B．4.8

C．5.2　　　　　　　　　　　　　　　　　D．6

6、两个同心圆中，小圆的切线被大圆截得的线段长为6cm，该弦分大圆为3∶1的两部分，则大圆、小圆的半径分别为（　）

A．3,2　　　　　　　　　　　　　　　　　B．

C．3,1　　　　　　　　　　　　　　　　　D．

7、如图，AB、AC、CE都是⊙O的切线，B、D、E为切点，P为上一点，若∠A＋∠C=110°，则∠BPE等于（　）

A．70°　　　　　　　　　　　　　　　　 B．60°

C．50°　　　　　　　　　　　　　　　　 D．55°

8、如图，⊙O是△ABC的内切圆，若∠ACB=90°，∠BOC=105°，BC=20cm，则AC的长度为（　）

A．35cm　　　　　　　　　　　　　　　　 B．40cm

C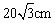．　　　　　　　　　　　　　　 D．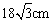

9、⊙O1与⊙O2半径之比为R∶r=4∶3，当O1O2=21cm时，两圆外切，当两圆内切时，O1O2的长度为（　）

A．O1O2＜3cm　　　　　　　　　　　　　　B．O1O2=3cm

C．3cm＜O1O2＜21cm　　　　　　　　　　　D．以上均错

10、已知⊙O1、⊙O2的半径分别为6和3，O1,O2的坐标分别为(5,0)和(0,6)，则两圆的位置关系是（　）

A．相交　　　　　　　　　　　　　　　　 B．外切

C．内切　　　　　　　　　　　　　　　　 D．外离