1、列一元二次方程解应用题的特点
列一元二次方程解应用题是列一元一次方程解应用题的继续和发展
从列方程解应用题的方法来讲，列出一元二次方程解应用题与列出一元一次方程解应用题是非常相似的，由于一元一次方程未知数是一次，因此这类问题大部分都可通过算术方法来解决．如果未知数出现二次，用算术方法就很困难了，正由于未知数是二次的，所以可以用一元二次方程解决有关面积问题，经过两次增长的平均增长率问题，数学问题中涉及积的一些问题，经营决策问题等等．
2、列一元二次方程解应用题的一般步骤
和列一元一次方程解应用题一样，列一元二次方程解应用题的一般步骤是：“审、设、列、解、答”．
(1)“审”指读懂题目、审清题意，明确已知和未知，以及它们之间的数量关系．这一步是解决问题的基础；
(2)“设”是指设元，设元分直接设元和间接设元，所谓直接设元就是问什么设什么，间接设元虽然所设未知数不是我们所要求的，但由于对列方程有利，因此间接设元也十分重要．恰当灵活设元直接影响着列方程与解方程的难易；
(3)“列”是列方程，这是非常重要的步骤，列方程就是找出题目中的等量关系，再根据这个相等关系列出含有未知数的等式，即方程．找出相等关系列方程是解决问题的关键；
(4)“解”就是求出所列方程的解；
(5)“答”就是书写答案，应注意的是一元二次方程的解，有可能不符合题意，如线段的长度不能为负数，降低率不能大于100%等等．因此，解出方程的根后，一定要进行检验．
3、数与数字的关系
两位数=(十位数字)×10＋个位数字
三位数=(百位数字)×100＋(十位数字)×10＋个位数字
4、翻一番
翻一番即表示为原量的2倍，翻两番即表示为原量的4倍．
5、增长率问题
(1)增长率问题的有关公式：
增长数=基数×增长率
实际数=基数＋增长数
(2)两次增长，且增长率相等的问题的基本等量关系式为：
原来的×(1＋增长率)增长期数=后来的
(1)上述相等关系仅适用增长率相同的情形；
(2)如果是下降率，则上述关系式为：
原来的×(1－增长率)下降期数=后来的
6、利用一元二次方程解几何图形中的有关计算问题的一般步骤
(1)整体地、系统地审读题意；
(2)寻求问题中的等量关系(依据几何图形的性质)；
(3)设未知数，并依据等量关系列出方程；
(4)正确地求解方程并检验解的合理性；
(5)写出答案．
7、列方程解应用题的关键
(1)审题是设未知数、列方程的基础，所谓审题，就是要善于理解题意，弄清题中的已知量和未知数，分清它们之间的数量关系，寻求隐含的相等关系；
(2)设未知数分直接设未知数和间接设未知数，这就需根据题目中的数量关系正确选择设未知数的方法和正确地设出未知数．
列方程解应用题应注意：
(1)要充分利用题设中的已知条件，善于分析题中隐含的条件，挖掘其隐含关系；
(2)由于一元二次方程通常有两个根，为此要根据题意对两根加以检验．即判断或确定方程的根与实际背景和题意是否相符，并将不符合题意和实际意义的根舍去．
例1、两个连续奇数的积为323，求这两个数．
思路：
(1)表示两个连续奇数的方法是：①2n＋1，2n－1；②2n－1，2n－3；③2n＋1，2n＋3；…(n表示整数)；(2)设元，①设较小的奇数为x，则另一个奇数为x＋2；②设较小的奇数为x－1，则另一个奇数为x＋1；③设较小的奇数为2n－1，则另一个奇数为2n＋1．
解法1：
设较小的奇数为x，另一个为x＋2．
根据题意将x(x＋2)=323 整理后得
x2＋2x－323=0，
解这个方程得：x1=17，x2=－19，
由x=17得x＋2=19，由x=－19得x＋2=－17
答：这两个数是17，19或者－19，－17．
解法2：
设这两个奇数为x－1和x＋1，
根据题意可得(x－1)(x＋1)=323，整理后
得x2=324，x=±18
当x=18时，18－1=17，18＋1=19
x=－18时，－18－1=－19，－18＋1=－17
答：两个奇数分别是17，19或者－19，－17．
解法3：
设较小的奇数为2x－1，较大的奇数为2x＋1
根据题意得(2x－1)(2x＋1)=323
整理后得x2=81
解得x1=9，x2=－9．
当x1=9时，这两个数是17，19．
当x2=－9时，这两个数是－19，－17．
答：两个奇数分别为17、19或－19、－17．
总结：
对于一些数学问题，若能根据题目的基本特征和特殊因素，进行多角度的观察，分析联想，便可发现多种思维通路，得到多种不同的解法，使之妙趣横生，令人大开眼界．巧设元就是如此，三种不同的设元，列出三种不同的方程，得出不同的x的值，结果“殊途同归”．比较一下，哪种方法最优．
例2、一个两位数，个位数字与十位数字之和为5，把个位数字与十位数字对调后，所得的两位数与原来的两位数的乘积为736，求原来的两位数．
思路：
数与数字之间的关系是：两位数=(十位数字)×10＋(个位数字)
解题的关键是正确地写出原来的两位数与对调后的两位数，为了便于分析，可列出下表：
解：
设原两位数的十位数字为x，则个位数字为(5－x)，根据题意得
[10x＋(5－x)][10(5－x)＋x]=736
整理得x2－5x＋6=0
解这个方程得x1=2，x2=3
当x=2时，5－x=3，两位数为23；
当x=3时，5－x=2，两位数为32．
总结：(1)对于多位数问题要善于用各数位上的数字来表示该多位数；
(2)求出方程的解之后，要善于检验它们是否符合题意，不要漏解，更不能保留不合题意的解．
例3、在一次象棋比赛中，实行单循环赛制(即每个选手都与其他选手比赛一局)，每局赢者记2分，负者记0分，如果平局，两个选手各记1分，今有4个同学统计了比赛中全部选手的得分总和，结果分别为2005、2004、2070、2008，经核实确定只有一位同学统计无误，试计算这次比赛中共有多少名选手参赛．
思路：
(1)先分析比赛的总局数，假设此次比赛共有x名选手参赛，则共比赛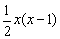
局；
(2)再分析得分总和的特征，由于无论胜、负、平每一局比赛都记2分，则比赛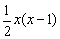
局的得分总和就是全部参赛选手的得分总和．即x(x－1)分，又x必为正整数，因此x与x－1是两个连续自然数的积，必为偶数，因此2005分属统计错误，其次两个自然数的积的个位数只可能是0，2，6．因此得分总和不可能是2004，2008，由条件知得分总和只可能是2070．
解：
设共有x(x为正整数)名选手参赛，所以共计有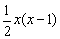
局比赛．因为每局比赛共记2分，所以全部选手的得分总和为x(x－1)分，由于相邻两个自然数之积是
