一、填空题
1、抛物线y=-3(x-1)2向上平移k个单位,所得抛物线与x轴交于点A1(x1,0)和B(x2,0).如果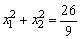 ,则k=_________. ,则k=_________.
2、二次函数y=ax2+b(a≠0)中,若当x取x1、x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值等于_________.
3、若把一条抛物线向上平移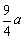 个单位(a>0),再向左平移 个单位(a>0),再向左平移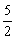 个单位,就得到第二条抛物线y=ax2.已知第一条抛物线经过点(0,4),那么第一条抛物线的函数关系式是_________. 个单位,就得到第二条抛物线y=ax2.已知第一条抛物线经过点(0,4),那么第一条抛物线的函数关系式是_________.
4、抛物线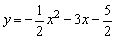 的对称轴是_________,顶点坐标是_________. 的对称轴是_________,顶点坐标是_________.
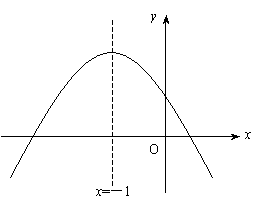
5、二次函数y=ax2+bx+c的图象如图所示,直线x=-1是它的对称轴,则a·b·c_______0,a∶b=_______.
6、当a=_________时,抛物线y=x2-ax+a-2与x轴的两交点的距离最小,其最小距离是_________.
7、不论自变量x取什么实数,二次函数y=2x2-6x+m的函数值总是正值,那么m的取值范围是_________.
[答案与提示]
二、选择题.
8、如果直线y=ax+b(ab≠0)不经过第三象限,那么抛物线y=ax2+bx的顶点是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
9、若二次函数y=ax2+4x+a-1的最小值是2,则a的值是( )
A.4 B.-1
C.3 D.4或-1
10、如图,抛物线y=ax2+bx+c与x轴相交于点A、B,与y轴相交于点C.如果OB=OC=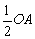 ,那么b的值为( ) ,那么b的值为( )
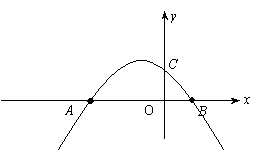
A.-2 B.-1
C.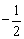 D. D.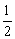
11、已知二次函数y=ax2+bx+c的图象如图所示,且OA=OC,则下列各式:①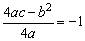 ;②ac+b+1=0;③abc>0;④a-b+c>0,其中正确的有( ) ;②ac+b+1=0;③abc>0;④a-b+c>0,其中正确的有( )
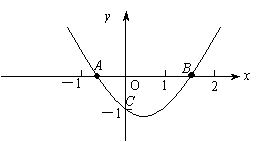
A.1个 B.2个
C.3个 D.4个
12、二次函数y=-x2+6x-7,当x取值为t≤x≤t+2时,此函数的最大值为y最大值=-(t-3)2+2,则t的取值范围为( )
A.t≤0 B.0≤t≤3
C.t≥3 D.都不对
13、二次函数y=x2-4x+3的图象交x轴于A、B两点,交y轴于点C,则△ABC的面积为( )
A.6 B.4
C.3 D.1
14、若一抛物线y=ax2与四条直线x=1,x=2,y=1,y=2围成的正方形有公共点,则a的取值范围是( )
A.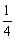 ≤a≤1 B. ≤a≤1 B.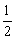 ≤a≤2 ≤a≤2
C.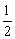 ≤a≤1 D. ≤a≤1 D.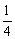 ≤a≤2 ≤a≤2
15、已知点A(1,y1),B(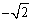 ,y2),C(-2,y3)在函数y=2(x+1)2- ,y2),C(-2,y3)在函数y=2(x+1)2-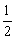 的图象上,则y1,y2,y3的大小关系是( ) 的图象上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y1>y3>y2
C.y3>y1>y2 D.y2>y1>y3
[答案与提示]
三、解答题.
16、已知抛物线y=x2-(a+2)x+9的顶点在坐标轴上.
(1)求a的值;
(2)当a>0时,该抛物线与直线y=x+9交于A、B两点,且A点在B点左侧.求点A和点B的坐标;
(3)P为(2)中线段AB上的点(A、B两端除外),过点P作x轴的垂线与抛物线交于点Q,线段AB上是否存在点P,使PQ的长等于6?若存在,请求出P点坐标?若不存在,说明理由.
[答案]
17、已知二次函数y=a(x+m)2+k(a≠0)的图象经过原点,当x=1时,函数y的最小值是-1.
(1)求这个二次函数的解析式,并在平面直角坐标系中画图象草图;
(2)若这个二次函数的图象与x轴交点为A、B,顶点为C,试判断△ABC的形状.
[答案]
18、点A是正比例函数y=2x和反比例函数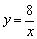 在第一象限的交点. 在第一象限的交点.
(1)求点A的坐标;
(2)如果直线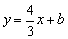 经过点A且与x轴交于点C,求b及点C的坐标; 经过点A且与x轴交于点C,求b及点C的坐标;
(3)如果已知点B(8,-12),求过A、B、C三点的二次函数的解析式.
[答案]
19、已知抛物线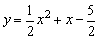 . .
(1)用配方法求它的顶点坐标和对称轴;
(2)若该抛物线与x轴的两个交点为A、B,求线段AB的长.
[答案]
20、抛物线y=ax2+bx+c过点A(-1,4),其顶点横坐标是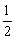 ,与x轴分别交于B(x1,0),C(x2,0)两点(其中x1<x2),且 ,与x轴分别交于B(x1,0),C(x2,0)两点(其中x1<x2),且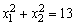 . .
(1)求抛物线的解析式及顶点E的坐标;
(2)设此抛物线与y轴交于点D,点M是抛物线上的点.若△MBO的面积为△DOC面积的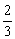 倍,求点M的坐标. 倍,求点M的坐标.
[答案]
|