例1、（2001年，陕西）如图所示，⊙O1、⊙O2外切于点A，外公切线BC与⊙O1切于点B，与⊙O2切于点C，与O1O2的延长线交于点P，已知∠P=30°．

（1）求⊙O1与⊙O2半径的比；

（2）若⊙O1半径为2cm，求及外公切线BC所围成的图形（阴影部分）的面积．

分析：（1）利用圆的切线性质和半径的关系；

　　　（2）阴影部分的面积转化为梯形与扇形的面积的差

解：（1）连结O1B，O2C．过O1作O1D⊥O2C，则O1BCD为矩形.

∴O2D=r2－r1．O1O2=r1＋r2，∠O2O1D=∠P=30°，

∴r1＋r2=2(r2－r1)，∴r2=3r1，∴r1︰r2=1︰3．

（2）∵r1=2(cm)，∴r2=6(cm)，∴O2D=4(cm)，O1O2=8(cm)．

∴BC=O1D=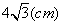，且∠BO1O2=120°,∠O1O2=60°．

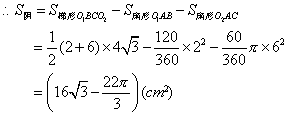
例2、(2002·宁夏回族自治区)圆锥的母线长为5cm，高为3cm，在它的侧面展开图中，扇形的圆心角是___________．

分析：圆锥的底面半径为，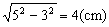

　　　底面周长即侧面展开图中扇形的弧长为2×4π＝8π(cm)，

　　　设扇形的圆心角为n°，则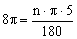，n＝288°．

答案：288°．

注意：圆锥的母线长即为侧面展开图中扇形的半径．

例3、(2002·山东省济宁市)如图，扇形的圆心角∠AOB＝135°，C为扇形上一点，且∠BOC＝45°，设扇形BOC，三角形AOC，弓形AmC的面积分别为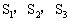，则它们之间的大小关系(用“>”表示)是__________．

分析：∵∠AOB＝135°，∠BOC＝45°，∴∠AOC＝90°．

　　　设扇形的半径为R，则

　　　，

　　　，

　　　．

　　　∵，

　　　∴．

答案：．

注意：本题还可试用估算的方法来比较两个无理数的大小．

-END-