|
主讲:方敏文
一周强化
一、一周知识概述
1、圆的定义
(1)形成性定义:在一平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.固定的端点O叫做圆心,线段OA叫做半径.记作“⊙O”,读作“圆O”.
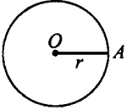
(2)集合性定义:圆是平面内到定点的距离等于定长的点的集合,其中,定点是圆心,定长是圆的半径.
2、与圆有关概念
(1)弦:连结圆上任意两点间的线段叫做弦.
(2)直径:经过圆心弦,称为直径.
注意:直径是最长的弦,直径是弦,但弦不一定是直径.
(3)弧:圆上任意两点间的部分叫做圆弧,简称弧,以A、B为端点的弧用“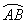 ”表示.读作“弧AB”.能够重合的两条弧叫做等弧. ”表示.读作“弧AB”.能够重合的两条弧叫做等弧.
小于半圆周的弧叫做劣弧,大于半圆周的弧叫做优弧.
在同圆或等圆中,相等的弧所对的弦相等;相等的弦所对的优弧和劣弧分别相等.
(4)半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
等圆:能够重合的两个圆叫做等圆.半径相等的两个圆是等圆.
2、圆的对称性
圆是轴对称图形,任何一条直径所在直线都是它的对称轴.圆也是中心对称图形,圆心是它的对称中心.
注意:圆有无数条直径,所以圆有无数条对称轴.
3、垂径定理及推论
定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于这条弦,并且平分弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦。
4、圆心角
圆心角:顶点在圆心的角叫做圆心角.
5、圆心角、弧、弦之间的关系
定理:在同圆或等圆中,相等的圆心角所对的弦相等,所对的弧也相等;相等的弦或相等的弧所对的圆心角相等.
推论:在同圆或等圆中,如果两个圆心角、两条弧或两条弦中有一组量相等,那么它们所对的其余各组量分别相等.
注意:(1)在具体运用定理或推论解决问题时可根据需要,选择有关部分,比如“等弧所对圆心角相等”,“在同圆或等圆中,相等的圆心角所对的弧相等”等.
(2)不能忽略“在同圆或等圆中”这个前提条件,若没有这一条件,虽然圆心角相等,但所对的弧、弦不一定相等.
(3)结合图形深刻理解圆心角、弧、弦这几个概念与“所对”一词的含义.
(4)若无特殊说明,定理推论中“弧”一般指劣弧.
6、圆周角
(1)圆周角:顶点在圆上,两边和圆相交的角叫做圆周角.
半圆或直径所对的圆周角都相等,都等于90°(直角).90°的圆周角所对的弧是圆的直径.
(2)圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
二、重难点知识归纳
重点:垂径定理、三组量之间的关系、圆周角定理.
难点:以上定理的综合应用.
三、典例剖析
例1、如图所示,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不一定成立的是( )
A.CM=DM B.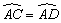
C.AD=2BD D.∠BCD=∠BDC
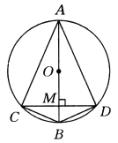
分析:
因为AB是⊙O的直径,且AB⊥CD,所以根据垂径定理可知CM=DM,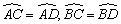 。从而根据“在同圆(或等圆)中,相等的弧所对的弦相等”,可知AC=AD,BC=BD,所以△BCD为等腰三角形,即∠BCD=∠BDC。而AD与BD的数量关系是不确定的,故正确答案为C。 。从而根据“在同圆(或等圆)中,相等的弧所对的弦相等”,可知AC=AD,BC=BD,所以△BCD为等腰三角形,即∠BCD=∠BDC。而AD与BD的数量关系是不确定的,故正确答案为C。
答案:C
例2、已知圆内接△ABC中,AB=AC,圆心O到BC距离为6cm,圆的半径为10cm.求腰AB的长.
分析:
分两种情况:圆心O在△ABC内和△ABC外,利用垂径定理结合勾股定理求解.
解:
第一种情况:如图(甲),过点A作AD⊥BC于D,连结OB.
∵AB=AC,∴BD=DC.∴AD垂直平分BC.
∴AD过圆心O.∴AD=AO+OD=10+6=16(cm).
在Rt△OBD中,BD2=OB2-OD2=102-62=64(cm).
在Rt△ABD中,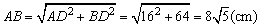 . .
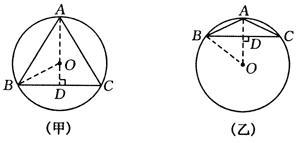
第二种情况:如图(乙),过点A作AD⊥BC于点D,连结OB.
和第一种解法相同,可得AD过圆心O,
∴AD=OA-OD=10-6=4(cm).
在Rt△ABD中,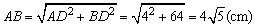 . .
综合得腰长AB为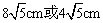 . .
点评:
这是一道结论开放性试题,解答时要根据已知和未知,结合图形进行分类讨论,多角度、多方位思考,以培养思维的严密性.
例3、如图所示,AB,CD是⊙O的两条弦,且AB//CD,直径MN⊥AB,根据垂径定理,请你至少写出五个结论.
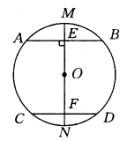
分析:
由MN⊥AB,MN为直径,可得AE=BE,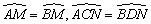 .由MN⊥AB,AB//CD,可得MN⊥CD,CF=DF, .由MN⊥AB,AB//CD,可得MN⊥CD,CF=DF,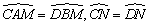 .又由 .又由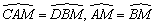 ,可得 ,可得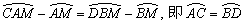 . .
解:
正确的结论有:AE=BE,CF=DF,MN⊥CD,
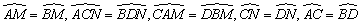 . .
小结:
由本例我们得出垂径定理的一个重要推论,即圆的两条平行弦所夹的弧相等。如图所示,若AB//CD,则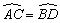 。 。
例4、已知:如图,A点是半圆上一个三等份点,B点是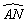 的中点,P是直径MN上一动点,⊙O的半径为1,则AP+BP的最小值是多少? 的中点,P是直径MN上一动点,⊙O的半径为1,则AP+BP的最小值是多少?
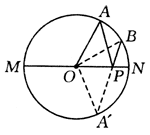
分析:
利用圆的对称性,将AP+BP转化为一条线段的长.结合弧与圆心角的关系得到直角三角形是解题的关键.
解:
作A关于MN的对称点A′,根据圆的对称性,则A′必在圆上.
连结BA′交MN于点P,连结PA,则PA+PB最小,此时PA+PB=PA′+PB=A′B.
连结OA′、OB.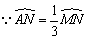 ,∴∠AON=∠A′ON=60°. ,∴∠AON=∠A′ON=60°.
又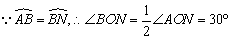 .∴∠A′OB=90°. .∴∠A′OB=90°.
 . .
即PA+PB的最小值是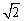 . .
例5、如图,四边形ABCD的四个顶点在⊙O上,且对角线AC⊥BD,OE⊥BC于E.求证: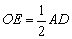 . .
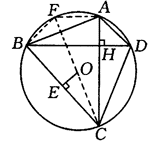
证明:作直径CF,连结AF、BF.
∵OE⊥BC,∴E为BC的中点.
又∵CF为直径,O为圆心,
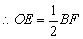 .(三角形中位线定理) .(三角形中位线定理)
∵CF为直径,∴∠CAF=90°,即FA⊥AC.
又AC⊥BD,∴FA∥BD,
∴∠FAB=∠ABD.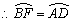 ,BF=AD. ,BF=AD.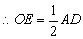 . .
点评:
由线段的倍分关系,容易想到三角形的中位线、垂径定理等知识.本例作直径,是使△BCF的中位线OE显现出来,再证BF=AD即可.
- 返回 -
|