主讲：金老师高级教师　余国琴

一周强化

一、一周知识概述

1、相似与轴对称、平移、旋转一样，也是图形之间的一个基本变换，可以将一个图形放大或缩小，保持形状不变．

　　位似图形：两个相似多边形，如果它们对应顶点所在的直线相交于一点，我们就把这样的两个图形叫做位似图形．

　　位似变换的定义：两个多边形不仅相似，而且对应顶点的连线相交于一点，像这样的相似叫做位似．这点O叫做位似中心．放映电影时，胶片和屏幕上的画面就形成一种位似关系，它们的位似中心是放映机上的灯光的点．

　　利用位似的方法，可以把一个多边形放大或缩小．

2、确定物体位置的两种方式

　　（1）建立适当的平面直角坐标系，用点的坐标来表示物体的位置．不同的坐标系，所表示的物体的坐标也不同．

　　（2）用相对于某物体的方向和角和距离来表示物体的位置

3、位似变换的点的坐标求法

　　在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或－k．

4、在同一坐标系中，图形经过平移、轴对称变换等变化，对应点的坐标变化规律

　　（1）图形沿x轴向右平移a个单位，点的纵坐标不变，点的横坐标增加a个单位；

　　图形沿x轴向左平移b个单位，点的纵坐标不变，点的横坐标减少b个单位；

　　（2）图形沿y轴向上平移c个单位，点的横坐标不变，点的纵坐标增加c个单位；

　　图形沿y轴向下平移d个单位，点的横坐标不变，点的纵坐标减少d个单位；

　　（3）点P（a，b）关于x轴对称的点的坐标是（a，－b）；即关于x轴对称的点，其横坐标相同，纵坐标互为相反数；

　　（4）点P（a，b）关于y轴对称的点的坐标是（－a，b）；即关于y轴对称的点，其纵坐标相同，横坐标互为相反数；

　　（5）点P（a，b）关于原点中心对称的点的坐标是（－a，－b）；即关于原点对称的点，其横纵坐标均互为相反数．

二、重难点知识

1、位似图形的理解

　　(1)位似图形必须满足：①是相似图形；②所有对应顶点的连线都经过同一点．

　　(2)位似比：位似图形是相似图形，所以有相似比，这个相似比就是位似比．

2、图形的相似与位似图形的区别与联系：

　　两个图形是相似图形，但不一定是位似图形；

　　两个图形是位似图形，它们一定是相似图形．

3、用位似法画相似的多边形，关键是确定位似中心，位似中心选在不同的位置，画相似的过程的繁简就不同．

4、位似中心也可以取在多边形内，或多边形的一边上、或顶点，下面是位似中心不同的画法．

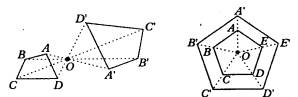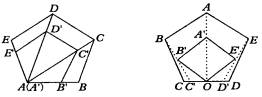
5、图形的放大与缩小要分类讨论

(1)纵坐标保持不变，横坐标分别变成原来的k倍．

①当k＞1时，原图形被横向拉长为原来的k倍．

②当0＜k＜1时，原图形被横向缩短为原来的k倍．

(2)横坐标保持不变，纵坐标分别变成原来的k倍．

①当k＞1时，原图形被纵向拉长为原来的k倍．

②当0＜k＜1时，原图形被纵向缩短为原来的k倍．

(3)纵坐标保持不变，横坐标分别加k．

①当k＞0时，原图形形状、大小不变，向右平移k个单位长度．

②当k＜0时，原图形形状、大小不变，向左平移|k|个单位长度．

(4)横坐标保持不变，纵坐标分别加k．

①当k＞0时，原图形形状、大小不变，向上平移k个单位长度．

②当k＜0时，原图形形状、大小不变，向下平移|k|个单位长度．

(5)横坐标保持不变，纵坐标分别乘以－1，所得图形与原图形关于x轴成轴对称．

(6)纵坐标保持不变，横坐标分别乘以－1，所得图形与原图形关于y轴成轴对称．

(7)横、纵坐标分别乘以－1，所得图形与原图形关于原点成中心对称．

(8)横、纵坐标分别变成原来的k倍(k≠±1)．

①当k＞1时，所得图形与原图形相似，形状不变，大小扩大到原来的k倍．

②当0＜k＜1时，所得图形与原图形相似，形状不变，大小缩小到原来的k倍．

三、典型例题讲解

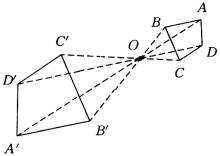
例1、如图所示，分别按下列要求作出四边形ABCD以O为位似中心的位似四边形A′B′C′D′．

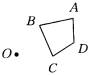
(1)沿OA方向放大为原图形的2倍；

(2)沿AO方向放大为原图形的2倍．

分析：

　　此题两问都是将原图形放大2倍，也就是位似比为2︰1，而(1)问是沿OA方向，即从O点向A点的方向放大；而(2)问是沿AO方向，即从A点向O点的方向放大．

解：(1)如图（1）所示．

　　①连接OA，并延长OA到A′，使A A′=OA．

　　②连接OB，并延长OB到B′，使BB′=OB．

　　③连接OC，并延长OC到C′，使CC′=OC．

　　④连接OD，并延长OD到D′，使DD′=OD．

　　⑤连接A′B′，B′C′，C′D′，D′A′．

　　则四边形A′B′C′D′是四边形ABCD关于O点的位似图形，且位似比为2︰1．

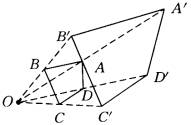
（1）　　　　　　　　　　　　　　　（2）

　　(2)如图（2）所示．

　　①连接AO，并延长AO到A′，使O A′=2OA．

　　②连接OB，OC，OD，并延长BO，CO，DO到B′，C′，D′，使OB′=2OB，OC′=2OC，OD′=2OD．

　　③连接A′B′，B′C′，C′D′，D′A′．

　　则四边形A′B′C′D′是四边形ABCD关于O点的位似图形，且位似比为2︰1．

例2、丽丽为自己设想并绘制了未来的大学校园的平面示意图，如图所示，你能根据她画的图回答下列问题吗?

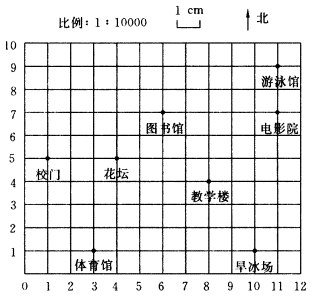
　　(1)花坛位于校门的什么方向上?到校门的图上距离为多少厘米?实际距离为多少米?

　　(2)花坛的北偏东45°方向上有什么建筑物?

　　(3)如果用(1，5)表示图上校门的位置，那么花坛、图书馆、游泳馆、电影院、教学楼、早冰场、体育馆的位置分别可以表示成什么?

分析：

　　本题(1)(2)两问渗透了用极坐标思想确定位置的方法；(3)问渗透了用直角坐标思想确定位置的方法．

解：(1)正东方向，3cm，300m．

　　(2)图书馆．

　　(3)花坛(4，5)，图书馆(6，7)，游泳馆(1l，9)，电影院(11，7)，教学楼(8，4)，旱冰场(10，1)，体育馆(3，1)．

注意：用一对数表示花坛、图书馆等位置时，应注意这对数是有序的．

例3、如图是某次海战中敌我双方舰艇对峙示意图，对我方舰艇来说：

（1）北偏东方向上有哪些目标？要想确定敌舰B的位置，还需要什么数据？

（2）距我方潜艇图上距离为1cm处的敌舰有哪几艘？

（3）要确定每艘敌舰的位置，各需要几个数据？

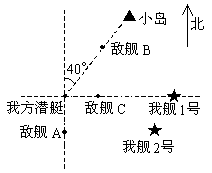
分析：本题以潜艇为观察点，确定敌舰的位置都是相对于我方潜艇而言的.

解：

　　（1）如图，对我方潜艇来说，北偏东40°的方向上有两个目标：敌舰B和小岛．

　　要想确定敌舰B的位置，仅用北偏东40°的方向是不够的，还需知道敌舰Ｂ距我方潜艇的距离.

　　（2）距我方潜艇图上距离1cm处的敌舰有两艘：敌舰A和敌舰C.

　　（3）要确定每艘敌舰的位置，各需要两个数据：距离和方位.如对我方潜艇来说，敌舰A在正南方向，图上距离为1cm处；敌舰B在北偏东40°，图上距离为1.4cm处；敌舰C在正东方向，图上距离为1cm处.

例4、将下图中的△ABC作下列变换，画出相应的图形，指出三个顶点的坐标所发生的变化．

　　(1)沿y轴负方向平移1个单位；

　　(2)关于x轴对称；

　　(3)以C点为位似中心，放大到1.5倍．

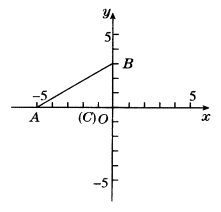
分析：

　　作平移、对称后的图形与原图全等，点的坐标发生变化，可根据平移、对称的特征，求出平移、对称变换后图形的坐标．位似变换如果以原点为位似中心可按位似变换的点的坐标求法求点的坐标．

解：变换后的图形如下图所示．

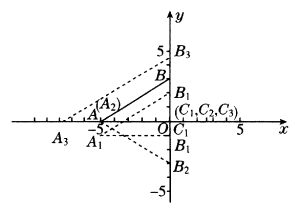
　　(1)将△ABC沿y轴负方向平移1个单位后得到△A1B1C1，A1(－5，－1)，B1(0，2)，C1(0，－1)．

　　即横坐标不变，纵坐标减小．

　　(2)将△ABC关于x轴对称后，得△A2B2C2，A2(－5，0)，B2(0，－3)，C2(0，0)．

　　即横坐标不变，纵坐标变为原来的相反数．

　　(3)将△ABC以C点为位似中心，放大到1.5倍得△A3B3C3，显然，A3(－5×1.5，0)，B3(0，3×1.5)，C3(0，0)，即A3(－7.5，0)，B3(0，4.5)，C3(0，0)．

反思：

　　本题应先按图形变换的要求画出相应的图形，再求出变换后图形的点的坐标，第(3)问求变换后图形的点的坐标的方法，注意此时的位似中心是原点．

例5、如图所示，在直角坐标系中，第一次将△OAB变化成△OA1B1，第二次将△OA1B1变化成△OA2B2……已知A(1，3)，A1(2，4)，A2(4，5)；B(2，0)，B1(4，0)，B2(8，0)，在总结三角形的顶点坐标变化规律的基础上，按此规律推测，将△OAB进行了n次变化后，各顶点An，O，Bn的坐标为多少？

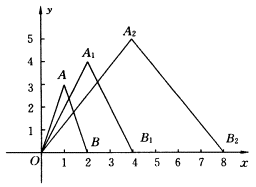
错解：

　　根据已知条件观察，An的横坐标的变化规律为1，2，4，…，2n－1，An的纵坐标的变化规律为3，4，5，…，n＋2，Bn的横坐标的变化规律为2，4，8，…，2n，纵坐标为0，所以An的坐标为(2n－1，n＋2)，Bn的坐标为(2n，0)．

解析：

　　原A点的坐标为(1，3)，即(20，3＋0)，第一次变化后A1点的坐标为(2，4)，即(21，3＋1)；

　　第二次变化后A2点的坐标为(4，5)，即(22，3＋2)，

　　由此推出，第n次变化后An点的坐标为(2n，3＋n)．

　　原B点的坐标为(2，0)，即(20＋1，0)，

　　第一次变化后B1的坐标为(4，0)，即(21＋1，0)，

　　第二次变化后B2的坐标为(8，0)，即(22＋1，0)，

　　由此推出第n次变化后Bn点的坐标为(2n＋1，0)．

- 返回 -