|
一周强化
一、一周知识概述
1、有序实数对
有顺序的两个数a与b组成的数对，叫有序实数对，记作（a,b）.利用数对可以准确地表示出一个位置.
2、常见的确定平面上的点位置常用的方法
（1）以某一点为原点（0，0）将平面分成若干个小正方形的方格，利用点所在的行和列的位置来确定点的位置．
（2）以某一点为观察点，用方位角、目标到这个点的距离这两个数来确定目标所在的位置.
3、平面直角坐标系的定义
在平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系，水平的数轴叫做x轴或横轴，铅垂的数轴叫y轴或纵轴，两数轴的交点O称为原点.
4、平面直角坐标系的结构
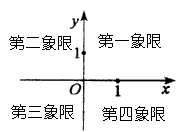
x轴和y轴把坐标平面分成四个部分，称之为四个象限，按逆时针顺序依次叫第一象限，第二象限，第三象限，第四象限.如图，坐标轴不属于任何象限.
5、点的坐标
在平面内一点P，过P向x轴、y轴分别作垂线，垂足在x轴、y轴上对应的数a，b分别叫P点的横坐标和纵坐标，则有序实数对（a,b）叫做P点的坐标.
6、坐标平面内的点P（a,b）的坐标特征：
象限
内的
点
|
点P在第一象限 |
a>0,b>0 |
点P在第二象限 |
a<0,b>0 |
点P在第三象限 |
a<0,b<0 |
点P在第四象限 |
a>0,b<0 |
坐标
轴上
的点
|
点P在x轴上：y=0,x为一切实数 |
点P在x轴正半轴上：a>0,b=0 |
点P在x轴负半轴上：a<0,b=0 |
点P在y轴上：x=0，y为一切实数 |
点P在y轴正半轴上：b>0,a=0 |
点P在y轴负半轴上：b<0,a=0 |
7、坐标平面上对称点的坐标特征
（1）关于x轴对称的两点的横坐标相同，纵坐标互为相反数；
（2）关于y轴对称的两点的纵坐标相同，横坐标互为相反数；
（3）关于原点对称的两点的横、纵坐标都互为相反数.
8、两坐标轴夹角的平分线上的点的坐标的特征
（1）第一、第三象限两坐标轴夹角的平分线上的点的横、纵坐标相等；
（2）第二、四象限两坐标轴夹角的平分线上的点的横、纵坐标互为相反数，一般记作（a,－a）.
坐标平面内的点和有序数对是一一对应的.
二、重难点知识归纳
1、有序实数对的定义
2、常见的确定平面上的点的位置常用的方法.
3、平面直角坐标系的概念.
4、点的坐标的意义.
5、两条坐标轴夹角平分线上的点的坐标的特征.
三、典型例题剖析
例1、如图，
 表示三经路与一纬路的十字路口，
 表示一经路与三纬路的十字路口，如果用(3,1)→(3,2)→(3,3)→(2,3)→(1,3)表示由到的一条路径，用同样的方式写出另外一条由到的路径：(3,1)→(______)→(______)→(______)→(1,3)．
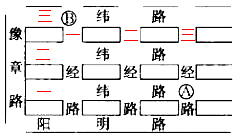
分析：
用数对表示路口的位置，前一个数表示南北向所在的第几个经路，后一个数表示东西向所在的第几纬路.
答案：
2，1；2，2；2，3(答案不惟一)
例2、如图是某次海战中敌我双方舰艇对峙示意图，对我方舰艇来说：
（1）北偏东方向上有哪些目标？要想确定敌舰B的位置，还需要什么数据？
（2）距我方潜艇图上距离为1cm处的敌舰有哪几艘？
（3）要确定每艘敌舰的位置，各需要几个数据？
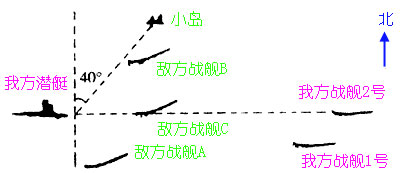
分析：
本题以潜艇为观察点，确定敌舰的位置都是相对于我方潜艇而言的.
解：
（1）如图，对我方潜艇来说，北偏东40°的方向上有两个目标：敌舰B和小岛．
要想确定敌舰B的位置，仅用北偏东40°的方向是不够的，还需知道敌舰Ｂ距我方潜艇的距离.
（2）距我方潜艇图上距离1cm处的敌舰有两艘：敌舰A和敌舰C.
（3）要确定每艘敌舰的位置，各需要两个数据：距离和方位.如对我方潜艇来说，敌舰A在正南方向，图上距离为1cm处；敌舰B在北偏东40°，图上距离为1.4cm处；敌舰C在正东方向，图上距离为1cm处.
例3、在直角坐标系中描出下列各点(-5,2)、(-4.5，-2)、(-3,-3)、(0,0)、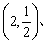 (3.5,1)、(6,0)，并将所得的点用线段顺次连结起来．观察所得的图形，你觉得它象什么？如果是一个星座的美丽图案，请指出其名称．
分析：
先在x轴上找出表示横坐标a的点，再在y轴上找出表示纵坐标b的点，过这两个点分别作x轴和y轴的垂线，垂线的交点就是点（a,b）.
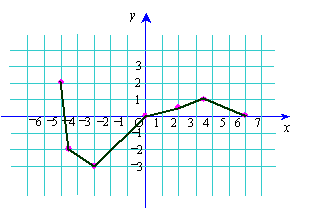
答案：如图，象勺子，北斗七星．
例4、（1）若点（5－a,a－3）在第一、三象限角平分线上，求a的值.
（2）已知两点A（－3,m）,B(n,4).若AB∥x轴，求m的值，并确定n的范围.
（3）点P到x轴和y轴的距离分别是3和4，求点P的坐标.
分析：
（1）中在一、三象限夹角平分线上的点的横坐标与纵坐标相等；
（2）与x轴平行的直线上的点的纵坐标相等；
（3）中的P点有多个.
解：
（1）因为点（5－a,a－3）在第一、三象限角的平分线上，所以5－a=a－3，所以a=4；
（2）因为AB∥x轴，所以m=4，因为A、B两点不重合，所以n≠－3；
（3）设点P的坐标为（x,y），由已知条件，得|y|=3,|x|=4，所以y=±3,x=±4.
所以P点坐标为（4，3）或（－4，3）或（4，－3）或（－4，－3）.
例5、已知点A（a－1,－2），B（－3,b＋1），根据以下要求确定a、b的值.
（1）直线AB∥y轴；
（2）直线AB∥x轴；
（3）A、B两点在第二、四象限两条坐标轴夹角的平分线上.
分析：
（1）两点连线平行y轴，这两点的横坐标相同，但纵坐标不相同；
（2）两点连线平行x轴，这两点的纵坐标相同，但横坐标不相同；
（3）当两点位于第二、四象限两坐标轴夹角的平分线上时，每个点的纵、横坐标都互为相反数.
解：
（1）∵直线AB∥y轴，∴a－1=－3,b＋1≠－2，
即a=－2,b≠－3.当a=－2且b≠－3时，直线AB∥y轴.
（2）∵直线AB∥x轴，∴b＋1=－2,a－1≠3,即b=－3,a≠－2.
当b=－3且a≠－2时，直线AB∥x轴.
（3）∵ 点A（a－1,－2），B（－3，b＋1）在第二、四象限两坐标轴夹角的平分线上，
则点M（x,y）中x＋y=0.
即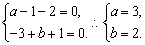
当a=3,b=2时，A、B两点位于第二、四象限两坐标轴夹角的平分线上.
- 返回 -
|
