相交线与平行线

同步教学

一、一周知识概述

（一）、知识点归纳

1、垂线

（1）当两条直线相交所成的四个角中有一个角为直角时，其他三个角也都成为直角，此时就说两条直线互相垂直，它们的交点叫做垂足。直线l1与l2垂直，记作“l1⊥l2”.

（2）垂线的画法可以概括为“一靠二落三画”.如图，“一靠”即用三角板的一条直角边靠在直线l1上，“二落”即使P点落在另一条直角边上，“三画”即过P点画出与l1垂直的直线l2.

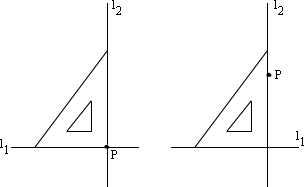
（3）通过画图，直观地得到：在同一平面内，经过直线外或直线上一点，有且只有一条直线与已知直线垂直。其中“有且只有”的含义是：“有”表示过一点垂直于已知直线的垂线总是存在的，不会没有，它表示存在性；“只有”表示这样的垂线是惟一的，不会有第二条，它表示惟一性。

（4）点到直线的距离是指点到直线的垂线段的长度.其中“长度”不可缺少.

（5）公理：垂线段最短。

2、同位角、内错角、同旁内角

（1）同位角、内错角、同旁内角的概念

　　两条直线被第三条直线所截，构成了八个角，也称“三线八角”。其中位置相同的一对角（两个角分别在两条直线的相同一侧，并且在第三条直线的同旁）叫做同位角。在两条直线之间，并且位置交错（即分别在第三条直线的两旁）的一对角，叫做内错角。在两条直线之间，并且在第三条直线的同旁的一对角，叫做同旁内角。

（2）同位角、内错角、同旁内角的识别

　　判别同位角、内错角、同旁内角的关键是找到三线，即找到两条直线和截这两条直线的第三条直线，所需判别的两个角的四条边应该分布在这三条直线上。在复杂的图形中判别这三类角时，应沿着角的两边将图形补全，或把多余的线暂时隐去，找到“三线八角”的图形，进而判定这两个角的位置关系。“ F型”为同位角，“Z型”为内错角，“U型”为同旁内角。

3、平行线

（1）平行线的概念

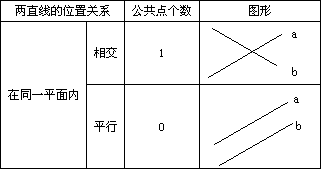
　　在同一平面内不相交的两条直线叫做平行线。直线 a平行于直线b，记作“a∥b”，读作“a平行于b”.满足：①在同一平面内，②不相交。两个条件，缺一不可。

（2）在同一平面内，两条直线的位置关系只有相交、平行两种。

（3）由画图可知：经过已知直线外一点，有且只有一条直线与已知直线平行.

（4）平行线的识别

①同位角相等，两直线平行；

②内错角相等，两直线平行；

③同旁内角互补，两直线平行。

（5）平行线的特征

①两直线平行，同位角相等；

②两直线平行，内错角相等；

③两直线平行，同旁内角互补。

另外，根据平行线的定义可知：如果两条直线平行，那么它们永远不相交。

（6）几何中，图形之间“位置关系”一般都与某种“数量关系”有着内在联系。常由“位置关系”决定其“数量关系”；反之也可以以“数量关系”去确定“位置关系”。正确区分平行线的识别方法和特征是十分重要的。由角的相等或互补关系，得到两条直线平行的结论是识别方法；而由两条直线平行，得到角相等或互补关系的结论是特征。

（7）两条直线的位置关系的比较

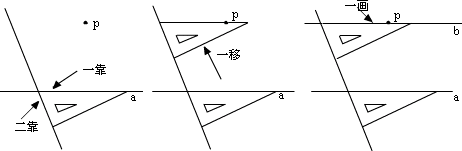
（8）用三角板、直尺画平行线时要“两靠一移一画”。即把三角板的一边靠在已知直线上，直尺靠在三角板的另一边上，这是“两靠”，“一移”即把三角板在靠在直尺的基础上移动，移动到经过已知点，最后画出所求直线，如图：

（二）、例题讲解

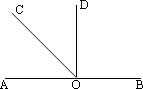
例 1、如图所示，O为直线AB上一点，OC把∠AOD平分，∠AOC=∠BOC；

（1）求∠COD的度数；

（2）试判断OD与AB的位置关系，并说明理由.

[解答]

例 2、如图，直线AB、CD、EF相交，①指出∠3与其它角（带标号的），是什么关系的角；②图中共有多少对同位角、内错角和同旁内角.

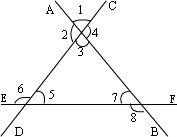
[解答]

例 3、已知∠1=72°，∠2=72°，∠3=60°，求∠4的度数.

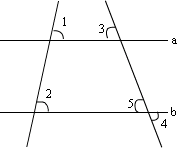
[解答]

例 4、如图，AB∥CD，BE平分∠ABC，CF平分∠BCD，你能发现BE和CF的位置有什么关系吗？

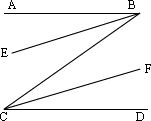
[解答]

例 5、如图所示，AB∥CD，∠1=∠2，∠BEF与∠EFC相等吗？为什么？

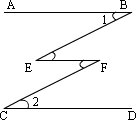
[解答]

- 返回 -