在线测试
二、填空题
9、内角和为1080°的多边形是__________边形.
10、若一个多边形每一个外角都为30°,则它的边数是____________.
11、若正多边形一个内角是144°,则它是_________边形.
12、已知过m边形的一个顶点有7条对角线,n边形没有对角线,k边形共有k 条对角线,则(m-k)n=_____________.
13、用边长都相等的正三角形、正方形、正六边形铺满地面(你选择一种正多边形或二种正多边形),其方案有_______种,分别是________________.
14、某足球场需铺设草皮,现有正三角形、正五边形、正六边形、正八边形、正十边形5种形状的草皮,请你帮助工人师傅选择两种草皮来铺设足球场,可供选择的两种组合是____________________.
15、一个八边形,如果它的每个内角都相等,那么它的内角等于________.
16、若一个n边形的边数增加一倍,则内角和将__________________.
[答案与提示]
三、解答题
17、有两个各内角都相等的多边形,它们的边数之比为1:2,且第二个多边形的内角比第一个多边形的内角大15°,求这两个多边形的边数.
[答案与提示]
18、某同学计算多边形内角和时,得到的答案是1340°,老师指出他把某一个外角也加了进去. 你能知道这个同学计算的是几边形的内角和?而他多加的那个外角是多少度呢?
[答案与提示]
19、如图,求图中∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数之和.

[答案与提示]
20、一个多边形木板在不影响其他角的大小情况下,截去一个角,得到的新多边形木板的内角和是3240°,求原多边形的内角和.
[答案与提示]
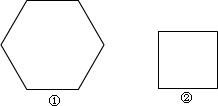
21、图①为正八边形瓷砖,这种形状的瓷砖能不能铺成平整、无空隙的地面?为什么?若加上一种边长与它相等的正方形瓷砖(如图②),能不能铺成?请你试试看,把你想到的方案画成草图.
[解答]
-END-