例1、希腊数学家丢番图趣题 今有四数,取其每三个数相加,则其和分别为22,24,27和20,求这四个数各是多少?
解:设四个数之和为x,则22+24+27+20=3x, x=31,
31-22=9,31-24=7,31-27=4,31-20=11.
这四个数分别为9,7,4,11.
点拨:由于每三个数的和已知,所以从它们的和考虑,宜采用设整体变量.
例2、父子二人同在一家工厂工作,父亲从家里走到工厂要用30分钟,儿子走这段路只要20分钟,某天父亲比儿子早5分钟动身上班,问过多少分钟儿子才能追上父亲?
解:设儿子出发x分钟后追上父亲,又设儿子每分钟走m米,则父亲每分钟走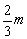 米.依题意,得: 米.依题意,得: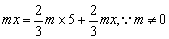 ,∴两边可同时约去m,解得x=10. ,∴两边可同时约去m,解得x=10.
点拨:由于距离一定时,速度与时间成反比,于是有“父速:儿速=20:30”即父速=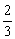 ×儿速,这是本题的隐含条件,据此可增设辅助未知数.可见,有些较复杂的应用题,往往条件隐含,关系交错,这时在直接设未知数的同时,可再增设辅助未知数,架起连接已知量与未知量的桥梁,以便理顺各个量之间的关系,建立方程,这些辅助未知数一般可以在求解过程中消去. ×儿速,这是本题的隐含条件,据此可增设辅助未知数.可见,有些较复杂的应用题,往往条件隐含,关系交错,这时在直接设未知数的同时,可再增设辅助未知数,架起连接已知量与未知量的桥梁,以便理顺各个量之间的关系,建立方程,这些辅助未知数一般可以在求解过程中消去.
|