|
一、一周知识概述
本周学习了双曲线的两种定义,推导了双曲线两种标准方程,并要求能用待定系数法求双曲线的标准方程.在数学思想和研究方法上与学习椭圆时类似,所以学习中可与椭圆的相关知识进行对比,注意它们的联系和区别.接下来学习了利用双曲线的标准方程,研究双曲线的几何性质及性质的应用,最后又学习了应用这些知识解决有关双曲线的综合问题.学习这些内容的时候,通过类比椭圆几何性质的研究方法,可以自主探究双曲线的范围、对称性、顶点、离心率等几何性质,提高类比分析归纳的能力.
二、重、难点知识讲解
1、双曲线的定义(第一定义)
平面上,到两定点F1、F2的距离之差的绝对值为一常数2a(2a<|F1F2|)的点M的轨迹为一双曲线.
注意:
(1)“在平面上”说明双曲线亦是平面曲线.
(2)常数2a应满足“小于|F1F2|=2c”的时候,轨迹才是双曲线;
当2a=2c时,M点轨迹为两条射线;
当2a>2c时,M点不存在.
(3)要注意是差的绝对值,否则只是双曲线的一支;
(4)由定义可得双曲线上所有点的性质,即||MF1|-|MF2||=2a.
要学会运用此性质.
例1、若椭圆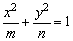 (m>n>0)和双曲线 (m>n>0)和双曲线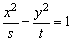 (s、t>0)有相同的焦点F1和F2,而P是这两条曲线的一个交点,则|PF1|·|PF2|的值为多少? (s、t>0)有相同的焦点F1和F2,而P是这两条曲线的一个交点,则|PF1|·|PF2|的值为多少?
[解析]
2、双曲线的标准方程(中心在原点、焦点在坐标轴上的双曲线的方程)
如果双曲线的焦点在x轴上,标准方程为 (a>0,b>0) (a>0,b>0)
如果双曲线的焦点在y轴上,标准方程为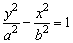 (a>0,b>0). (a>0,b>0).
双曲线标准方程中a>0,b>0,但a不一定大于b.如果x2的系数是正的,那么焦点在x轴上,如果y2的系数是正的,那么焦点在y轴上,有别于椭圆通过比较分母的大小来判定焦点的位置.要学会利用题设条件求a、b并判断焦点所在的坐标轴求双曲线方程,或用待定系数法确定双曲线方程;另外,在方程Ax2+By2=C中,只要AB<0,且C≠0,方程表示双曲线方程.
例2、求适合下列条件的双曲线的标准方程.
(1)c=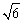 ,经过点(5,-2),焦点在x轴上; ,经过点(5,-2),焦点在x轴上;
(2)a=2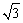 ,且与双曲线 ,且与双曲线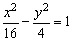 有公共焦点; 有公共焦点;
(3)焦点在x轴上的双曲线过点P(4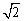 ,-3),且(0,5)与两焦点的连线互相垂直. ,-3),且(0,5)与两焦点的连线互相垂直.
[解析]
3、双曲线的几何性质
(1)双曲线的几何性质包括:范围、对称轴、对称中心及其实轴与虚轴的概念、焦距与焦点坐标、离心率、准线、渐近线方程等.
关于双曲线渐近线方程的记忆,只须将双曲线标准方程中的1改为0即可.如双曲线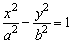 的渐近线方程为 的渐近线方程为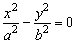 ,即 ,即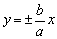 ,这两条直线恰是边长2a、2b的矩形的两条对角线所在的直线.当双曲线的两支向外延伸时,与这两条直线无限接近,但永不相交. ,这两条直线恰是边长2a、2b的矩形的两条对角线所在的直线.当双曲线的两支向外延伸时,与这两条直线无限接近,但永不相交.
渐近线是双曲线特有的性质,理解渐近线的渐近性,可以理解为: ,当x无限增大时, ,当x无限增大时, 无限接近于0,所以y无限趋近于 无限接近于0,所以y无限趋近于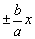 . .
(2)等轴双曲线x2-y2=±a2的渐近线方程是y=±x,离心率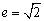 . .
(3)离心率的求解注意运用几何性质,将相关线段关系转化为a、b、c的齐次等式.
(4)与双曲线 有相同渐近线的方程是 有相同渐近线的方程是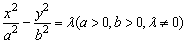 . .
4、要掌握双曲线的第二定义:
在平面上到一定点F的距离与到一定直线距离之比为一个大于1的常数e的点的轨迹.即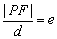 .教材例5即是应用双曲线的第二定义 .教材例5即是应用双曲线的第二定义
几何性质见下表:
标准方程 |
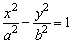 (a>0,b>0) (a>0,b>0)
|
 (a>0,b>0) (a>0,b>0)
|
图形 |

|

|
范围 |
|x|≥a,y∈R |
|y|≥a,x∈R |
对称性 |
对称轴:x轴、y轴,对称中心:原点 |
离心率 |
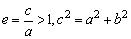
|
顶点 |
(-a,0)(a,0) |
(0,-a),(0,a) |
焦点 |
(-c,0)(c,0) |
(0,-c)(0,c) |
准线 |

|
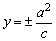
|
渐近线 |
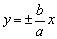
|

|
例3、经过双曲线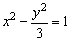 的右焦点F2作倾斜角为30°的弦AB, 的右焦点F2作倾斜角为30°的弦AB,
(1)求|AB|.
(2)F1是双曲线的左焦点,求△F1AB的周长.
[解析]
例4、已知双曲线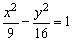 的右焦点F,点A(9,2),试在这个双曲线上求一点M,使|MA|+ 的右焦点F,点A(9,2),试在这个双曲线上求一点M,使|MA|+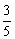 |MF|的值最小,并求出这个最小值. |MF|的值最小,并求出这个最小值.
[解析]
4、直线与双曲线的位置关系
(1)一次方程与二次方程所表示的是直线与曲线的位置关系,一般处理方法均是将一次方程代入二次方程考查解的个数,但这里直线方程代入双曲线方程后当二次项为零时,即是直线与渐近线平行时,有一个交点,然后讨论△与零的大小判断解的个数.
直线与圆锥曲线相交的弦长问题
(2)直线l︰y=kx+b,与二次曲线C︰(x, y)=0交于A、B两点,由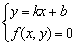 得:ax2+bx+c=0 (a≠0),则 得:ax2+bx+c=0 (a≠0),则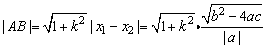 . .
(3)利用“点差法”来解决中点弦问题,其基本思路是设点(即设出弦的端点坐标)——代入(即将端点代入曲线方程)——作差(即两式相减)——得出中点坐标与斜率的关系。
(4)圆锥曲线中的对称问题
对于曲线上点关于直线的对称问题处理时要抓住三点:
(1)对称点的连线垂直于对称轴(垂直);
(2)对称点的连线段的中点在对称轴上(平分);
(3)对称点所在直线与曲线相交(△>0)。
例5、当k为任值时,直线y=kx-1与双曲线①没有公共点;②有两个公共点;③只有一个公共点.
[解析]
例6、已知双曲线方程3x2-y2=3.
(1)求以定点A(2,1)为中点的弦所在直线方程;
(2)以定点B(1,1)为中点的弦存在吗?若存在,求出其所在直线方程;若不存在,请说明理由.
[解析]
5、有关双曲线的综合应用问题
涉及到双曲线综合题,同学们要注意定义、几何性质以及函数,不等式等知识的综合运用.
例7、已知双曲线 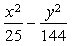 =1 的左、右焦点分别为F1、F2,左准线为 =1 的左、右焦点分别为F1、F2,左准线为 ,能否在双曲线的左支上求一点 P, 使| PF1| 是P到L的距离 d与| PF2| 的等比中项? 若能成等比中项,求出点P的坐标;若不能,请说明理由. ,能否在双曲线的左支上求一点 P, 使| PF1| 是P到L的距离 d与| PF2| 的等比中项? 若能成等比中项,求出点P的坐标;若不能,请说明理由.
[解析]
例8、已知梯形ABCD中,|AB|=2|CD|,AB∥CD,点E分有向线段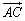 所成的比为 所成的比为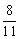 ,双曲线过C、D、E三点,且以A、B为焦点,求双曲线的离心率. ,双曲线过C、D、E三点,且以A、B为焦点,求双曲线的离心率.
[解析]
|