1、用向量处理平行问题
空间图形的平行关系包括直线与直线平行，直线与平面平行，平面与平面平行，它们都可以用向量方法来研究．
(1)设a、b是两条不重合的直线，它们的方向向量分别为a，b，那么a∥b
a∥b．
根据实数与向量积的定义：a∥b
a=kb．(k∈R，k≠0)
(2)平面与平面平行可转化为两个平面的法向量平行．
设两个不重合的平面α，β的法向量分别为a，b，那么α∥β
a∥b．
(3)直线与平面平行可以转化为直线的方向向量与平面的法向量垂直．
设直线l在平面α外，a是l的一个方向向量，b是α的一个法向量，那么l∥α
a⊥b
a·b=0．
(4)a∥平面α 
表示以a为方向向量的直线与平面α平行或在平面α内，因此也可由共面向量定理证明线面平行问题．
例1、底面为正三角形的斜棱柱ABC—A1B1C1中，D为AC的中点，求证：AB1∥平面C1BD．
分析：欲证AB1∥平面C1BD，可证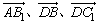
共面．
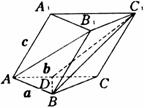
证明：
如图，记AB=a，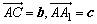
，则
，
∴
，
∴
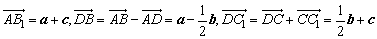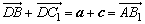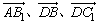共面．
∵B1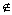
平面C1BD，
∴AB1∥平面C1BD．
2、用向量处理垂直问题
空间的线线、线面、面面垂直关系，都可以转化为空间两个向量的垂直问题来解决．
(1)设a，b分别为直线a，b的一个方向向量，那么a⊥b
a⊥b
a·b=0；
(2)设a，b分别是平面α，β的一个法向量，那么α⊥β
a⊥b
a·b=0；
(3)设直线l的方向向量为a，平面α的法向量为b，那么l⊥α
a∥b．
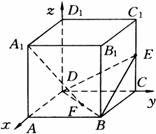
例2、在正方体ABCD—A1B1C1D1中，E、F分别是CC1、BD的中点．求证：A1F⊥平面BDE．
分析：
若用一般法证明，易证A1F⊥BD，而证A1F⊥DE或A1F⊥EF则较难，用向量法证明可化难为易．
证明：
如图，取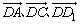
分别为x轴、y轴、z轴建立直角坐标系，设正方体的棱长为2．
A(2,0,0)，B(2,2,0)，A1(2,0,2)，E(0,2,1)，F(1,1,0)
则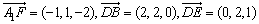
．
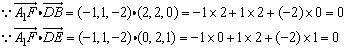
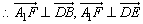，即A1F⊥DB，A1F⊥DE
∴A1F⊥平面BDE．
3、用向量处理角的问题
在立体几何中，涉及的角有异面直线所成的角、直线与平面所成的角、二面角等．关于角的计算，均可归结为求两个向量的夹角．
对于空间向量a，b，有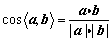
．利用这一结论，我们可以较方便地处理立体几何中的角的问题．
例3、如图，三棱柱OAB—O1A1B1，平面OBB1O1⊥平面OAB，∠O1OB=60°，∠AOB＝90°，且OB=OO1=2，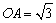
．
求：(1)二面角O1—AB—O的大小；
(2)异面直线A1B与AO1所成角的大小．
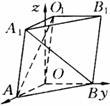
分析：
(1)求二面角大小可以转化为求两个平面法向量夹角的大小．
(2)转化为求
的夹角的大小．
解：
(1)以O为原点，分别以OA，OB所在直线为x,y轴，过O点且与平面AOB垂直的直线为z轴，建立空间直角坐标系．如图，则O(0,0,0)，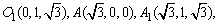
B(0,2,0)，
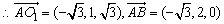
显然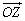
为平面AOB的法向量取n1=(0,0,1)．
设平面O1AB的法向量为n2=(x,y,z)，则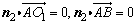
．
即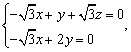
令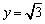
，x=2，z=1．
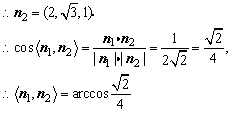
故二面角O1—AB—O的大小为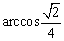
．
(2)设异面直线A1B与AO1，所成角为β，则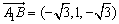
，
，
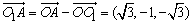设异面直线A1B与AO1所成角的大小为β
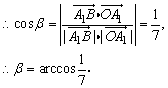
即异面直线A1B与AO1所成角的大小为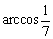
．
评注：
本题第(1)小题可由三垂线定理作出二面角O1—AB—O的平面角，通过解三角形求解，需要“作、证、算”三个基本步骤，而用坐标法解题过程基本上程序化，易于求解．
4、用向量处理距离问题
立体几何中涉及的距离问题较多，如两点距离，点与线的距离，点、线与平面的距离，两异面直线的距离等，它是一个难点，若用向量来处理这类问题，则思路简单，解法固定．
(1)利用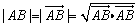
可以求解有关距离问题．
(2)设e是直线l上的一个单位方向向量，线段AB在l上的投影是A′B′，则有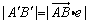
，由此可求点到线，点到面的距离问题．
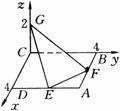
例4、如图，已知ABCD是边长为4的正方形，E，F分别是AD，AB的中点，GC垂直于ABCD所在的平面且GC=2，求点B到平面EFG的距离．
分析：
求点到平面距离，一般方法是先由该点向平面引垂线确定垂足，把点到平面的距离转化为解三角形求解，需要作辅助线，然后通过逻辑推理论证及计算，比较麻烦，而用向量法则较为简便．
解：
以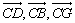
的方向分别为x轴，y轴，z轴的正方向建立直角坐标系，则G(0,0,2)、B(0,4,0)、A(4,4,0)、D(4,0,0)、E(4,2,0)、F(2,4,0)．
．
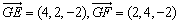设n0=(x,y,z)是平面EFG的单位法向量，则有
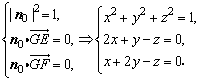
取z＞0，得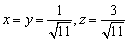
．
．
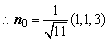又∵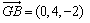
，
．
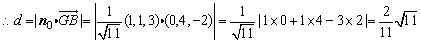即点B到平面EFG的距离为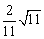
．
评注：
若平面α的斜线AO交α于点O，e是α的单位法向量，则A到平面α的距离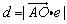
．
