|
一、一周知识概述
本周主要学习曲线的参数方程、圆锥曲线的参数方程、圆的参数方程、渐开线与摆线等内容,重点学习了参数方程的概念,参数方程与普通方程的互化,参数方程的几何意义等,并且要学会利用参数方程解题.
二、重难点知识归纳
(一)曲线的参数方程
1、参数方程的概念
一般地,在平面直角坐标系中,如果曲线上任意一点的坐标x,y都是某个变数t的函数
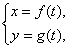 ① ①
并且对于t的每一个允许值,由方程组②所确定的点M(x,y)都在这条曲线上,那么方程②就叫做这条曲线参数方程,联系变数x,y的变数t叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.
2、圆的参数方程
方程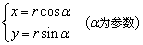 表示圆心在原点O,半径为r的圆的参数方程. 表示圆心在原点O,半径为r的圆的参数方程.
方程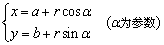 表示圆心在(a,b),半径为r的圆的参数方程. 表示圆心在(a,b),半径为r的圆的参数方程.
3、参数方程和普通方程的互化
一般地,是通过消去参数而从参数方程得到普通方程.
(二)圆锥曲线的参数方程
1、椭圆的参数方程
对于椭圆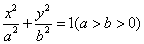 ,其参数方程为 ,其参数方程为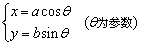 . .
即方程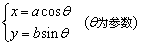 表示中心在原点O,焦点在x轴上的椭圆. 表示中心在原点O,焦点在x轴上的椭圆.
注意:参数θ是椭圆上一点所对应的圆的半径的旋转角,不是此点与原点连线的旋转角.
2、双曲线的参数方程
对于双曲线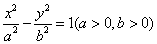 ,其参数方程为 ,其参数方程为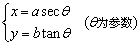 . .
即方程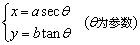 表示中心在原点,焦点在x轴上的双曲线. 表示中心在原点,焦点在x轴上的双曲线.
3、抛物线的参数方程
设抛物线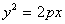 ,其参数方程为 ,其参数方程为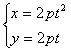 ,设动点P的坐标为( ,设动点P的坐标为(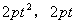 ). ).
O为抛物线顶点,可得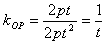 ,即 ,即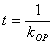 ,t的几何意义是过抛物线顶点的动弦斜率的倒数. ,t的几何意义是过抛物线顶点的动弦斜率的倒数.
(三)直线的参数方程
经过点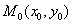 ,倾斜角为α的直线l的参数方程为 ,倾斜角为α的直线l的参数方程为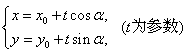 . .
三、典型例题剖析
例1、已知对于圆x2+(y-1)2=1上任意一点P(x,y),不等式x+y+m≥0恒成立,求实数m的取值范围.
[解析]
例2、已知点P在圆O′: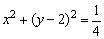 上移动,点Q在椭圆x2+4y2=4上移动,求|PQ|的最大值及相应的点Q的坐标. 上移动,点Q在椭圆x2+4y2=4上移动,求|PQ|的最大值及相应的点Q的坐标.
[解析]
例3、已知过抛物线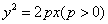 顶点O的弦OA所在的直线方程为 顶点O的弦OA所在的直线方程为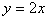 ,弦OB和弦OA垂直,且弦AB长为 ,弦OB和弦OA垂直,且弦AB长为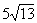 ,求p的值. ,求p的值.
[解析]
例4、已知椭圆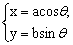 ( (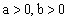 , ,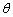 为参数)上的点P(x,y),求:(1)x、y的取值范围;(2)3x+4y的取值范围. 为参数)上的点P(x,y),求:(1)x、y的取值范围;(2)3x+4y的取值范围.
[解析]
例5、设抛物线过两点A(-1,6)和B(-1,-2),对称轴与x轴平行,开口向右,直线y=2x+7被抛物线截得的线段长是4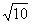 ,求抛物线方程. ,求抛物线方程.
[解析]
|