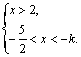不等关系与不等式　　一元二次不等式及其解法

同步教学

一、一周知识概述

　　本周学习不等关系与不等式、一元二次不等式及其解法．首先学习不等关系与不等式的性质，通过具体情境，感受在现实世界和日常生活中存在着大量的不等关系，理解不等式（组）对于刻画不等关系的意义和价值；掌握求解一元二次不等式的基本方法，并能解决一些实际问题；体会不等式、方程及函数之间的联系。利用一元二次函数的图象及一元二次方程求解一元二次不等式；

二、重难点知识归纳

1、用不等号连接起来的式子表示不等关系，这样的式子叫不等式．

不等式的常用的基本性质

（1）a>b，b>ca>c

(2)a>ba＋c>b＋c

(3)a>b，c>0ac>bc

(4)a>b，c<0ac<bc

2、一元二次不等式、一元二次函数与一元二次方程的关系

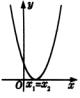
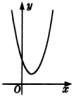
判别式 二次函数的图象
一元二次方程的根	有两根异实根	有两相等实根	没有实根
的解集			R
的解集

3、一元二次不等式的解法

　　解一元二次不等式的步骤：

　　（1）将原不等式化成一般形式（或），把二次项的系数变为正数（如果是负，那么在不等式两边都乘以－1，把系数变为正）．

　　（2）求出对应的一元二次方程的根．（先看能否因式分解，若不能，再看△，然后求根）

　　（3）根据一元二次函数的图象、二次方程的根确定一元二次不等式的解集．（根据一元二次方程的根及不等式的方向）

三、典型例题剖析

例1、解不等式．

分析：

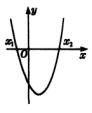
　　令f（x)= ，△＞0，即方程=0有两个不相等的实根，又图象开口向上，画出图象的示意图，由二次函数的零点和一元二次方程的根的关系知不等式的解集．

解：

　　因为△＞0，方程=0的根是

　　．

　　所以不等式的解集是{x|x<－，或x>2}．

例2、已知不等式ax2＋5x＋b＞0的解为，求 a，b．

分析：

　　不等式ax2＋5x＋b＞0的解为，则知二次函数y=ax2＋5x＋b的两个零点是x1=，x2=，由二次函数的零点与一元二次方程的关系知x1=，x2=是方程ax2＋5x＋b=0的两个实数根，由根与系数的关系得到关于a，b的方程组．

解：

　　因为不等式ax2＋5x＋b＞0的解为，所以x1=，x2=是方程ax2＋5x＋b=0的两个实数根，所以解得

例3、已知不等式x2－ax－b<0的解集是{x|2<x<3}，求不等式bx2－ax－1>0的解集．

分析：

　　一元二次不等式的解集是由一元二次方程的根及首项系数的正、负，不等式是大于还是小于零确定的，不等式x2－ax－b<0的解集是{x|2<x<3}，则x=2，x=3是方程x2－ax－b＝0的两根，求出a，b再解不等式．

解：

　　因为不等式x2－ax－b<0的解集是{x|2<x<3}，从而 a=2＋3=5，b=－(2×3)=－6，

　　于是－6x2－5x－1>0，即6x2＋5x＋1<0．

　　因△>0，方程 6x2＋5x＋1=0 的两根为：

　　

　　故所求不等式的解集为．

小结：

　　解一元二次不等式时，首先一定要使二次项系数为正数，其次要知道解集是由方程的根来给出，从而知道解集时，可求不等式系数．

例4、假设国家收购某种农副产品的价格是120元/担，其中征税标准是每100元征税8元（叫做税率是8个百分点，即8%），计划可收购m万担，为了减轻农民负担，决定税率降低x个百分点，预计收购量可增加2x个百分点，要使此项税收在税率降低后不低于原计划的78%，试确定x的取值范围．

分析：

　　此为应用题，关键是审好题，从中建立出数学模型进行求解．

解答：

　　税率降低后是(8－x)%，收购量为m(1＋2x%)万担，税收为120m(1＋2x%)(8－x)%万元，原来的税收为120m·8%万元，根据题意可得

　　120m（1＋2x%）(8－x)%≥120m·8%·78%，

　　即x2＋42x－88≤0，解之－44≤x≤2，

　　又 x>0，∴ 0<x≤2，∴x 的取值范围是{x|0<x≤2}．

例5、若不等式组的整数解只有－2，k应取怎样的值.

分析：针对第二个不等式的解集展开讨论．

解：

　　由，解得x<－1或x>2，再由，得　①

　　当时，，①的解为，这时原不等式组的解为，显然不包括－2，不合题意，舍去；

　　当时，，①的解为，这里原不等式组的解为

　　（Ⅰ），或（Ⅱ）

　　欲保证不等式组的解中只有整数解－2，由（Ⅰ）可得k<2，由（Ⅱ）可得k≥－3，即有－3≤k<2.

　　当，即时，①无解，此时，不等式组也无解.

　　综上所述，只有当时，原不等式组的整数解只有－2.

- 返回 -