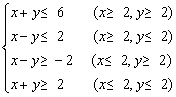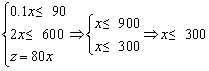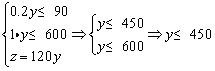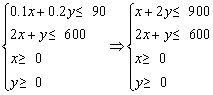二元一次不等式（组）与简单的线性规划问题

同步教学

主

一、一周知识概述

本周学习内容是用二元一次不等式表示区域和简单的线性规划问题．

　　（1）了解并会用二元一次不等式表示平面区域以及用二元一次不等式组表示平面区域；

　　（2）了解线性规化的意义以及线性约束条件、线性目标函数、线性规化问题、可行解、可行域以及最优解等基本概念；

　　（3）了解线性规化问题的图解法，并能应用它解决一些简单的实际问题；

　　（4）培养学生观察、联想以及作图的能力，渗透集合、化归、数形结合的数学思想，提高学生“建模”和解决实际问题的能力；探求解决线性规划实际问题的基本方法和步骤，培养学生的创新精神和应用能力．

二、重难点知识的归纳与剖析

1、二元一次不等式ax＋by＋c>0和ax＋by＋c＜0表示的平面区域．

　　（1）二元一次不等式ax＋by＋c>0在平面直角坐标系中表示直线ax＋by＋c=0某一侧所有点组成的平面区域．

　　把直线画成虚线以表示区域不包括边界直线，若画不等式ax＋by＋c≥0表示的平面区域时，此区域包括边界直线，则把边界直线画成实线．

　　（2）判断方法：由于对在直线ax＋by＋c=0同一侧的所有点（x,y），把它的坐标（x,y）代入ax＋by＋c，所得的实数的符号都相同，故只需在这条直线的某一侧取一个特殊点（x0,y0），以的正负情况便可判断ax＋by＋c>0表示这一直线哪一侧的平面区域，特殊地，当c≠0时，常把原点作为此特殊点．

2、简单的线性规划

　　（1）求线性目标函数的在约束条件下的最值问题的求解步骤是：

　　①作图——画出约束条件（不等式组）所确定的平面区域和目标函数所表示的平行直线系中的任意一条直线l；

　　②平移——将l平行移动，以确定最优解所对应的点的位置；

　　③求值——解有关的方程组求出最优点的坐标，再代入目标函数，求出目标函数的最值.

　　（2）在线性规划的实际问题中，主要掌握两种类型：一是给定一定数量的人力、物力资源，问怎样运用这些资源，能使完成的任务量最大，收到的效益最大；二是给定一项任务，问怎样安排，能使完成这项任务耗费的人力、物力资源量最小．不管是哪种类型，解线性规划的实际问题，关键在于根据条件写出线性的约束条件及线性目标函数，然后作出可行域，在可行域内求出最优解.

　　（3）寻找整点最优解的方法

　　①平移找解法：

　　先打网格，描整点，平移直线l，最先经过或最后经过的整点便是最优整点解，这种方法应充分利用非整点最优解的信息，结合准确的作图才行，当可行域是有限区域且整点个数又较少时，可逐个将整点坐标代入目标函数求值，经比较求最优解.

　　②调整优值法：

　　先求非整点最优解及最优值，再借助不定方程的知识调整最优值，最后筛选出整点最优解.

三、典型例题讲解

例1、画出不等式2x＋y-6＜0表示的平面区域

分析：

　　先画出直线，将原点代入看是否符合不等式，如符合，则在含原点的部分，否则，

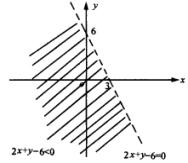
　　在不含原点的部分．

解：

　　先画直线2x＋y-6=0（画线虚线）,取原点（0，0），代入2x＋y-6，∵2x＋y-6＜0，∴  原点在不等式2x＋y-6＜0表示的平面区域内，不等式2x＋y-6＜0表示的平面区域如图阴影部分．

例2、画出不等式组：表示的平面区域.

分析：

　　在不等式组表示的平面区域是各个不等式所表示的平面点集的交集，因而是各个不等式所表示的平面区域的公共部分．本题的问题关键在于正确地描绘出边界直线，然后根据给出的不等式，判断出所表示的平面区域，为此必须分别画出每个不等式所表示的平面区域，然后取各平面区域的公共部分.

解答：

　　不等式x<3表示直线x=3左侧点的集合.

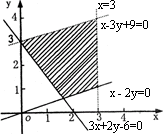
　　不等式2y≥x即x－2y≤0表示直线x－2y=0上及左上方点的集合.

　　不等式3x＋2y≥6，即3x＋2y－6≥0表示直线3x＋2y－6=0上及右上方点的集合.

　　不等式3y<x＋9即x－3y＋9>0表示直线x－3y＋9=0右下方点的集合.

　　综上可得：不等式组表示的平面区域如图所示的阴影部分.

小结：

　　（1）解决类似本题的问题时，先应对每一个不等式所表示的平面区域作出正确的判断，保证不因某一不等式所表示的平面区域产生失误，其次应注意所表示的平面区域是否包括了边界．

　　（2）画二元一次不等式表示的平面区域常用的方法是：直线定界、原点定“域”，即先画出对应的直线，再将原点坐标代入直线方程中，看其值比零大还是比零小；不等式组表示的平面区域是各个不等式所表示的平面点集的交集，是它们平面区域的公共部分.

例3、求不等式|x－2|＋|y－2|≤2所表示的平面区域的面积.

分析：

　　解答本题的关键是正确作出不等式所表示的平面区域，可先通过讨论去掉绝对值符号，再作图.

解答：

　　原不等式等价于

　　

　　作出其所表示的平面区域，如下图所示，它是边长为的正方形，面积等于8.

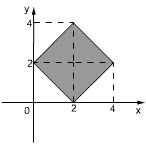
点评：

　　正确画出不等式表示的区域，观察图形的特殊性，是解决本题的关键所在．

例4、解线性规划问题：求z=3x＋y的最大值，使式中的x,y满足约束条件.

分析：

　　按照解线性规划问题的步骤解题．第一步：在平面直角坐标系中作出可行域；第二步：在可行域中找到最优解所对应的点；第三步：解方程的最优解，从而求出目标函数的最大值或最小值．

解答：

　　作出可行域，如图五边形OABCD所表示的平面区域．

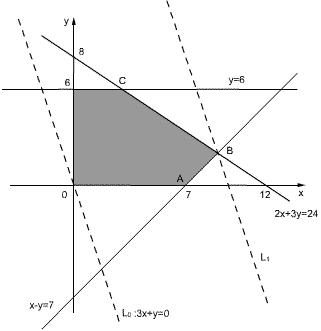
　　作出直线l0:3x＋y=0将它平移至点B，显然B的坐标是可行域中的最优解，它使z=3x＋y达到最大值．解方程组得B点的坐标为（9，2）.

　　∴zmax=3×9＋2=29．

点评：

　　 若目标函数设为z=x＋3y，约束条件不变，则z的最大值在点C（3,6）处取得.事实上，可行域内最优解对应的点在何处，与目标函数z=ax＋by(a≠0,b≠0)，所确定的直线l0：ax＋by=0的斜率有关．就这个例子而言，当l0的斜率为负数时，即时，若（直线2x＋3y=24的斜率）时，线段BC上所有点都使z取最大值（如本例）；当时，点C处使z取最大值（比如z=x＋3y），若，请同学思考．

例5、某家具厂有方木90m3，五合板600m2，准确加工成书桌和书橱出售．已知生产每张书桌需要方木料0.1m3，五合板2m2，生产每个书橱需要方木料0.2m3、五合板1m2，出售一张书桌可获利润80元，出售一个书橱可获利120元，如果只安排生产书桌，可获利润多少元？如果只安排生产书橱，可获利多少元？怎样安排生产可使所得利润最大？

分析：

　　（1）问什么，设什么，建立目标函数.

　　（2）根据已知条件列出不等式组，找出可行域.

解析：

　　（1）设只生产书桌x张，可获利润z元.

　　则

　　所以当x=300时，zmax=80·300=24000（元）.

　　即如果只安排生产书桌，最多可生产300张书桌，获得利润24000元.

　　（2）设只生产书橱y张，可获利润z元.

　　

　　所以当x=450时，zmax=120·450=54000（元）.

　　如果只安排生产书橱，最多可生产450个书橱，获得利润54000元.

　　（3）设生产书桌x张、书橱y个，利润总额为z元.

　　则

　　z=80x＋120y.

　　在直角坐标平面内作出上面不等式组所表示的平面区域，即可行域.

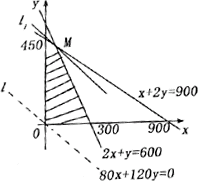
　　作直线l：80x＋120y=0，即直线2x＋3y=0.

　　把直线l向右上方平移到l1的位置时，直线经过可行域上的点M，此时z=80x＋120y=0取得最大值.

　　由

　　解得点M的坐标为（100，400）.

　　所以当x=100，y=400时，zmax=80·100＋120·400=56000（元）

　　因此，生产书桌100张、书橱400个，可使所得利润最大.

小结：

　　线性规划问题在解决实际问题时，要注意条件.

- 返回 -