纵观十几年的高考题,有关组合的题目常以“几何问题”、“产品质量抽检问题”“集合问题”“人或物的有关分配问题”等形式出现,常用分类思想,用直接法、间接法,一般以选择题或填空题考查.
例1、(2005天津高考)从集合{1,2,3,…,11}中的任意取两个元素作为椭圆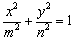 方程中的
方程中的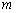 和
和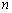 ,则能组成落在矩形区域
,则能组成落在矩形区域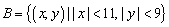 内的椭圆的个数是( )
内的椭圆的个数是( )
A、43 B、72 C、86 D、90
解析:
根据题意,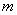 是不大于10的正整数、
是不大于10的正整数、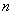 是不大于8的正整数。但是当
是不大于8的正整数。但是当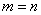 时
时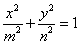 是圆而不是椭圆。先确定
是圆而不是椭圆。先确定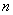 ,
,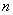 有8种可能,对每一个确定的
有8种可能,对每一个确定的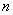 ,
,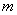 有
有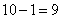 种可能。故满足条件的椭圆有
种可能。故满足条件的椭圆有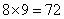 个。
个。
答案:B
例2、(2005全国高考Ⅱ)在由数字0,1,2,3,4,5所组成的没有重复数字的四位数中,不能被5整除的数共有_____________个.
解法一:
(直接法)不能被5整除的有两种情况:情况1、首位为5有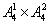 种,情况2、首位不是5的有
种,情况2、首位不是5的有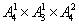 种,故在由数字0,1,2,3,4,5所组成的没有重复数字的四位数中,不能被5整除的数共有
种,故在由数字0,1,2,3,4,5所组成的没有重复数字的四位数中,不能被5整除的数共有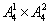 +
+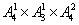 =192(个).
=192(个).
解法二:
(间接法)由0,1,2,3,4,5所组成的没有重复数字的四位数共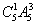 =300个,其中能被5整除的数分为两类:第一类,个位是0的有
=300个,其中能被5整除的数分为两类:第一类,个位是0的有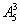 =60个;第二类,个位是5的有
=60个;第二类,个位是5的有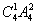 =48个,故符合条件的共300-60-48=192个.
=48个,故符合条件的共300-60-48=192个.
答案:192
例3、(2005北京高考)北京《财富》全球论坛期间,某高校有14名志愿者参加接待工作,若每天早、中、晚三班,每4人,每人每天最多值一班,则开幕式当天不同的排班种数为( )
A.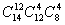 B.
B.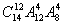 C.
C.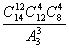 D.
D.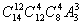
解析:
本题可以先从14人中选出12人即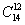 ,然后从这12人中再选出4人做为早班即
,然后从这12人中再选出4人做为早班即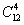 ,最后再从剩余的8人选出4人安排为中班即
,最后再从剩余的8人选出4人安排为中班即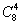 ,剩下的4个安排为晚班,以上为分步事件,应用乘法原理可得不同的排法为
,剩下的4个安排为晚班,以上为分步事件,应用乘法原理可得不同的排法为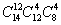 .
.
答案:A
点评:
排列组合中的分步计数原理与分类计数原理做为解决此类问题的基础.
例4、(2001年上海)某餐厅供应客饭,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种,现在餐厅准备了5种不同的荤菜,若要保证每位顾客有200种以上的不同选择,则餐厅至少还需要准备不同的素菜_______种.
解析:
设餐厅至少还要准备x种不同的素菜,则有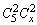 ≥200,∴
≥200,∴ 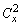 ≥20.
≥20.
故x的最小值为7.
答案:7