|
一周强化
一、一周知识概述
本周主要学习了二项式定理,用时五课时.主要内容有二项展开式,二项展开式的通项,二项式系数等.
二、重难点讲解
1、二项式定理
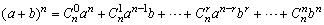 (n∈N+). (n∈N+).
公式右边的多项式叫做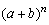 的二项展开式. 的二项展开式.
二项展开式的通项公式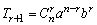 . .
说明:(1)二项展开式具有以下特征:
①项数:共有n+1项;
②系数:依次为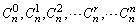 ; ;
③指数:a的指数从n起依次减少1,直到0为止;b的指数从0起依次增加1,直到n为止;各项a,b的指数之和恒为n.
(2)通项表示二项展开式中的任意项,只要n与r确定,该项也随之确定;公式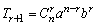 表示的是第r+1项,而不是第r项;公式中的a,b的位置不能颠倒,它们的指数和一定为n. 表示的是第r+1项,而不是第r项;公式中的a,b的位置不能颠倒,它们的指数和一定为n.
(3)a,b可以是单项式、多项式、分式、根式等.如
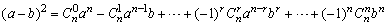 (n∈N*), (n∈N*),
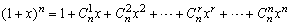 . .
例1、求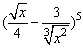 的展开式中的第4项的二项式系数,第4项的系数和含 的展开式中的第4项的二项式系数,第4项的系数和含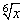 的项. 的项.
[解析]
例2、求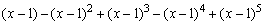 的展开式中x2的系数. 的展开式中x2的系数.
[解析]
2、二项式定理的应用
(1)利用二项式定理进行近似计算
利用二项式定理求幂的近似值,先将底数化为一个整数与一个绝对值较小的数的代数和,再利用二项式定理进行近似计算,关键是确定展开式中的保留项,使其满足近似计算的精确度.
(2)利用二项式定理解决整除问题.
利用二项式定理解决有关多项式的整除问题,关键是将所给多项式中的幂通过恒等变形变为二项式形式,使幂的底数两项中一项含有除式(或除式的因式),而另一项绝对值较小,然后展开证明.
例3、求0.955精确到0.01的的似值.
[解析]
例4、求证7777-1能被19整除.
[解析]
3、二项式系数的性质
(1)对称性:与首末两端“等距离”的两个二项式系数相等.
(2)增减性与最大值.如果二项式的幂指数是偶数,中间一项的二项式系数最大;如果二项式的幂指数是奇数,中间两项的二项式系数相等并且最大.
(3)二项式系数的和为2n,即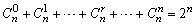 . .
说明:(1)这里是二项式系数(即组合数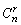 ,r=0,1,2,…,n)的性质,而不是二项展开式系数的性质. ,r=0,1,2,…,n)的性质,而不是二项展开式系数的性质.
(2)当n是偶数时,中间一项的二项式系数是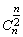 ;当n是奇数时,中间两项是 ;当n是奇数时,中间两项是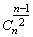 , ,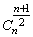 . .
(3)奇数项的二项式系数的和等于偶数项的二项式系数的和,即
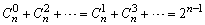 . .
(4)对二项式和其他恒等式中的字母赋值,就可得到各种不同的等量关系.
例5、已知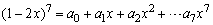 ,求: ,求:
(1)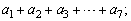
(2)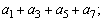
(3)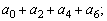
(4)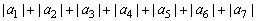 . .
[解析]
例6、(1+2x)n的展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项和系数最大的项.
[解析]
|