|
一周强化
一、一周内容概述
1、知道什么是单摆以及摆角很小时,单摆的振动是简谐运动
2、知道单摆的周期公式及其应用
3、了解等效摆长与等效加速度的概念
4、了解调节摆长可以改变钟的快慢
二、重点知识讲解
单摆的振动是一种比较特殊的简谐运动,对它的学习可以加深我们对简谐运动的理解。
(一)什么叫单摆
如图1所示,一条细线连着一个小球在竖直面内摆动,这种装置,就可以称为单摆。但是有两个条件:
1、摆线不可伸缩,摆线质量不计
2、摆球的直径远小于摆线的长度。
(二)什么情况下单摆的振动是简谐运动
如图2所示,单摆在平衡位置两侧来回摆动,在运动的过程中受到两个力的作用。
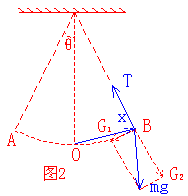
1、摆球的重力mg
2、摆线的拉力T
当小球运动到图2中,B位置时,其受力如图,将重力mg分解成两个力:
1、沿切线方向向下的分量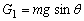
2、沿半径方向向外的分量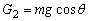
其中T、G2的方向均与运动方向垂直,不会产生回复力的效果。所以G1才是使单摆回到平衡位置的回复力。
在振幅很小(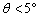 )的情况下。 )的情况下。
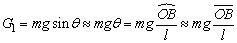
而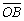 就是此时摆球偏离平衡位置的位移x,而且从图上也可以看出,两者的方向在偏角较小时正好相反。 就是此时摆球偏离平衡位置的位移x,而且从图上也可以看出,两者的方向在偏角较小时正好相反。
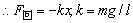
所以,在摆角较小的情况下(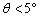 ),单摆的振动可以认为是简谐运动。 ),单摆的振动可以认为是简谐运动。
注意:图2中,G1不能认为等于重力G和拉力T的合力,因为T与G2一般不相等,不能抵消。一般情况下: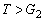 ,且 ,且
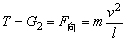
即T与G2的合力作为向心力。
特殊地:当单摆位于左、右两端最大位移位时,因为此时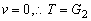
(三)单摆的周期公式及其应用
因为单摆的回复力F与位移x之间的正比例系数为k,所以,由简谐运动周期的一般公式,可得:
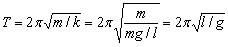
即单摆运动的周期为:
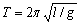
从该式中可以看出,单摆的周期只与摆长l及重力加速度有关,与振幅(即偏角)无关,这一性质叫做单摆的等时性。
将公式移项后,可以得出:
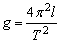
这是一种测量重力加速度的方法。
(四)等效摆长和等效加速度
对于一些特殊的摆,如图3所示:A为双线摆,B为圆弧面上的摆球,C为电梯内的单摆,其周期应如何运算?
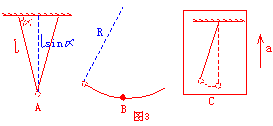
以上摆的周期的计算可以利用等效摆长和等效加速度的概念来解释:
对于A图,双线摆相当于一个摆长为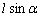 的单摆,所以它的周期为 的单摆,所以它的周期为
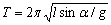
对于B图,它相当于一个摆长为R的单摆,所以它的周期为
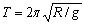
对于C图,在电梯中的单摆,当电梯加速上升时,因为此时摆球超重,其视重为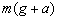 ,所以此时的等效加速度为 ,所以此时的等效加速度为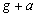 ,所以它的周期为 ,所以它的周期为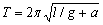
(五)改变钟的快慢
对于这一类问题,解决时抓住以下三点:
1、一摆钟的机械结构是固定的,所以不管是准确的钟还是不准的,摆锤摆动一次,钟面指示的时间都相同。
2、一段时间内摆锤的摆动次数:
准确钟 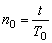
不准的钟 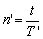
钟面上相应的批示时间为
准确钟 t
不准的钟 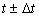 (“+”表示钟快;“-”代表钟慢) (“+”表示钟快;“-”代表钟慢)
3、同一时间内钟面指示时间之比等于摆动次数之比。
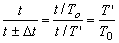
即钟面指示时间与钟的周期成反比。
特殊地,对于一昼夜而言,就有:
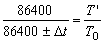
三、典型例题
例1、单摆的周期在下述情况下会变大的有:( )
A.摆锤质量增大
B.摆长减小
C.单摆从赤道移到北极
D.单摆从海平面移到高山
分析:
由单摆周期公式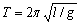 可以看出:周期T只与l及g有关,与摆锤质量无关,从赤道到北极,g增大,从海平面到高山,g减小,所以要使周期变大。应选D。 可以看出:周期T只与l及g有关,与摆锤质量无关,从赤道到北极,g增大,从海平面到高山,g减小,所以要使周期变大。应选D。
答案:D
例2、如图4所示,一单摆周期为T,( )则下列说法正确的是( ) )则下列说法正确的是( )
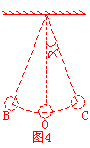
A.使摆球质量增加,则周期变小
B.使摆动的最大角度减小,则周期也变小
C.摆球由 运动时间为T/4 运动时间为T/4
D.摆球由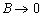 时速度增大,加速度减小。 时速度增大,加速度减小。
分析:
单摆的周期与振幅,质量无关,α变小只是振幅变小,故A、B错。
摆球由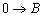 过程是 过程是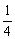 全振动,所以运动时间为 全振动,所以运动时间为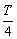
由B向0时,接近平衡位置,所以速度变大,回复力减小,加速度变小。
答案:C、D
例3、如图5所示,A、B两球放于一段光滑圆弧曲面上,它们与圆弧最低点O之间的弧长
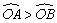 ,但均远小于圆弧半径。C球位于圆弧的圆心处,三球开始运动后,到达O点,所需时间的大小关系为:( ) ,但均远小于圆弧半径。C球位于圆弧的圆心处,三球开始运动后,到达O点,所需时间的大小关系为:( )
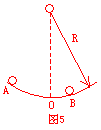
A.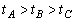 B. B.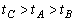
C.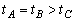 D. D.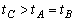
分析:
由于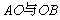 均远小于半径R,所以A、B球释放后均做简谐运动, 均远小于半径R,所以A、B球释放后均做简谐运动,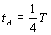 ,这一周期 ,这一周期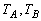 只与半径R、g有关,与振幅无关。s 只与半径R、g有关,与振幅无关。s
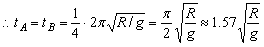
C球开始运动后应做自由落体运动。
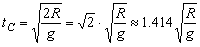
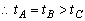
答案:C
例4、将地球上的秒摆(周期为2s的摆称为秒摆)拿到月球上去,它的振动周期变为多少?已知地球上重力加速度是月球的6倍。
分析:
秒摆从地球拿到月球,摆长不变,但g发生了变化,根据周期公式可求解:
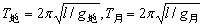
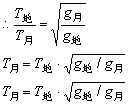
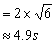
答:振动周期变为4.9s
说明:将单摆从地面转到其它天体上时,根据万有引力定律可知:
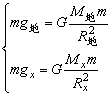
可得: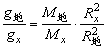
得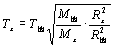
例5、在地面上有一单摆,周期为T,如果把此单摆放在该地的山顶上,山顶距地面的高度为地球半径的千分之一,则该单摆的周期变为多大?
分析:
当单摆的高度升高后,重力加速度将变小,从中可求出其周期的变化。
解:
在地球表面: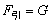
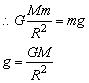
故到山上后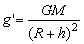
令山顶上周期为T′

由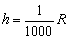
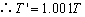
周期变为原来的1.001倍。
例6、已知悬挂在地面附近的摆长为l的单摆周期为T,地球半径为R,那么地球的密度是多少?
分析:
利用单摆的知识可以求出近地面的重力加速度,联系万有引力的知识,即可求出密度。
解:
由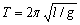 求出: 求出:
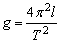
根据万有引力定律
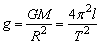
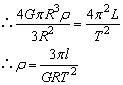
答:地球的密度为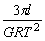
例7、北京和南京的重力加速度分别为 ,把在北京准确的摆钟拿到南京,它是快了还是慢了?一昼夜差多少?怎样调整? ,把在北京准确的摆钟拿到南京,它是快了还是慢了?一昼夜差多少?怎样调整?
分析:
由于从北京到南京,重力加速度减小,所以周期会变长,钟会变慢,要调快的话,就要将摆长减小。
解:
对于同一个钟,钟摆振动次数之比等于指针指示时间之比:
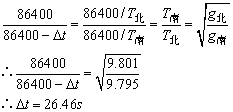
∴到南京后钟一昼夜要慢26.46s
为了调整走时,只要使摆钟在南京的周期与北京的周期一样。
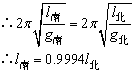
即要将摆长减少为原来的0.9994倍。 - 返回 -
|