|
一周强化
一、一周知识概述
本周主要通过演示实验,观察、分析有关波的反射和折射、波的衍射、波的干涉现象,及现象产生原因,结合波动规律解释和计算有关波的干涉问题。最后讨论有关多普勒效应。
二、重、难点知识归纳与讲解
(一)波的反射和折射
1、惠更斯原理:介质中的任一波面上的各点,都可以看作是发射子波的波源,其后任意时刻,这些子波在波前进方向的包络面就是新的波面。
2、用惠更斯原理来解释光的折射与反射。
(二)波的衍射:波可以绕过障碍物继续传播的现象。“闻其声不见其人”正是声波的衍射现象。(一切波都能发生衍射,衍射是波的特有现象。)
产生明显衍射现象必须具备一定的条件,障碍物或孔的尺寸跟波长差不多或比波长小.
说明:
①障碍物或孔的尺寸大小,并不是决定衍射能否发生的条件,仅是使衍射现象明显表现的条件.一般情况下,波长较大的波容易产生显著的衍射现象.
②波传到小孔(或障碍物)时,小孔(或障碍)仿佛一个新的波源,由它发出与原来同频率的波(称为子波)在孔后的传播,于是就出现了偏离直线传播方向的衍射现象.
③当孔的尺寸远小于波长时尽管衍射十分突出,但由于能量减弱,衍射现象不容易观察到.
(三)波的叠加原理
1、几列波相遇时各自保持原来运动状态,继续传播而不相互干扰。
如:教室内二人讲话,并不因为两声波相遇而改变原来的各自音调。
2、相遇区域各质点的振动位移为几列波单独引起的位移的矢量和。
3、波的干涉
(1)现象:两列同频率的波相遇,使某些区域振动加强,某些区域振动减弱,且加强与减弱区域互相间开。
(2)特点:
①振动的加强与减弱区相互间隔开,各质点振幅不同。
Amin=|A1-A2| Amax=|A1+A2| Amin≤A≤Amax
②加强区与减弱区域稳定,不随时间变化。
(加强区或减弱区是指振幅大小而言,该区域的各质点位移做周期性变化。)
③产生条件:(稳定的干涉图样)两列波同频率。
④现象分析:
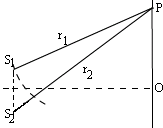
当两波源同向振动
若P点加强,则两波路程差: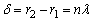 (λ为波长, n为正整数) (λ为波长, n为正整数)
若P点减弱,则两波路程差:
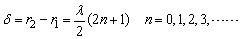
注意:若两波源反相位,则结论相反。
4、多普勒效应
(1)由于波源和观察者有相对运动,使观察者接收到的频率发生变化的现象,叫做多普勒效应。
①实例:运动火车的鸣笛声,光波的红移。
②实质:观察者接收到的频率发生了变化,而波源的频率并没有变化。
(2)多普勒效应的产生
①当波源和观察者相对静止时,接收频率不变
②当波源和观察者相互接近时,接收频率变大
③当波源和观察者相互远离时,接收频率变小
(3)多普勒效应是所有波的共性
(4)应用
①铁路工人判断火车车速和运行方向。
② 战士判断炮弹飞行方向。
③交通部分测车速。
④ 天文上判断星球远离。
三、典例分析
例1、如图是观察水面波衍射的实验装置,AC和BD是两块挡板,AB是一个孔,O是波源,图中已画出波源所在区域波的传播情况,每两条相邻波纹(图中曲线)之间距离表示一个波长,则波经过孔之后的传播情况,下列描述中正确的是( )
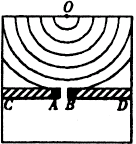
A.此时能明显观察到波的衍射现象
B.挡板前后波纹间距离相等
C.如果将孔AB扩大,有可能观察不到明显的衍射现象
D.如果孔的大小不变,使波源频率增大,能更明显观察到衍射现象
解析:
由图可知,此水面波的波长与孔AB的宽度相当,故可以观察到明显的衍射现象;若将孔AB扩大,使其宽度比波长大很多时,将不能观察到明显的衍射现象;若孔的大小不变,使波源的频率增大,由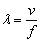 可知,波长λ将减小,f越大,λ越小,衍射现象越不明显。波绕过挡板发生衍射,挡板前后波纹间距离应保持不变,即波长不变(因v、f均款改变)。 可知,波长λ将减小,f越大,λ越小,衍射现象越不明显。波绕过挡板发生衍射,挡板前后波纹间距离应保持不变,即波长不变(因v、f均款改变)。
答案:ABC
例2、如图所示,S1、S2为频率相同的两个波源,以S1和S2为圆心的两组同心圆弧,分别表示同一时刻两列波的波峰(实线)和波谷(虚线),在图中标出了a、b、c、d、e五个点,其中e点是a、b连线的中点,那么下列说法正确的是( )

A.a是振动减弱的点,b是振动加强的点
B.c、d都是振动减弱的点
C.e是振动加强的点
D.e是振动减弱的点
E.e点振动方向向上
解析:
在波的干涉现象中,振动加强(或振动减弱)是指两列波叠加后质点振动的振幅比单独一列波使质点振动的振幅要大(或要小),因此,不能用质点在某时刻的位移大小来判断该质点振动的加强还是减弱的。其实,振动加强的点和振动减弱的点都在其平衡位置附近做周期性的振动,因此,某一时刻振动加强的点其位移有可能比振动减弱点的位移小,只是其振动的振幅要大些,振动更剧烈,振动最强点的振幅为两列波振幅之和,振动最弱点的振幅为两列波振幅之差。如图中的e点,此时刻的位移为零,但经过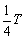 时,两列波都向前平移 时,两列波都向前平移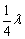 ,在e点出现波谷和波谷相遇,其振幅是两列波的振幅之和,故e点应是振动加强的点。由于波由a向b传播,故e点振动方向向下。 ,在e点出现波谷和波谷相遇,其振幅是两列波的振幅之和,故e点应是振动加强的点。由于波由a向b传播,故e点振动方向向下。
答案:BCE
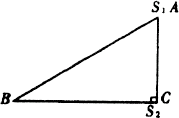
例3、如图所示,直角三角形ABC中,两直角边AC和BC的长分别为3m和4m,在A、C两点放着两个振动情况完全相同的波源S1和S2,其频率f=1360Hz,已知波源产生的波在空气中传播的速度为v=340m/s,则这两列波发生干涉,在BC边上振动最弱的点有______个。
解析:
由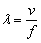 可得,这两列波在空气的波长均为 可得,这两列波在空气的波长均为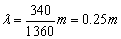 。考察BC边上的点到两波源的路程差△s,最大的是C点, 。考察BC边上的点到两波源的路程差△s,最大的是C点,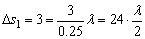 ;最小的是B点, ;最小的是B点,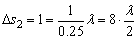 ,而同相干波发生干涉时,振动最弱点到两波源的路程差应是半波长的奇数倍,即 ,而同相干波发生干涉时,振动最弱点到两波源的路程差应是半波长的奇数倍,即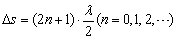 ,故只需判断8到24之间夹有多少个奇数即可。 ,故只需判断8到24之间夹有多少个奇数即可。
答案:8
例4、正在报警的警钟,每隔0.5s响一次,一列火车以60km/h的速度向警钟行驶,问坐在该列火车上的人在5min内能听到多少次钟声?已知声音在空气中传播的速度为320m/s。
解析:
要计算列车上的人在5min内能听到的钟声次声,就应先算出每秒钟接收到的声波的完全波的个数f。设该声波频率为f0,由于列车相对声波运动而增加的频率为△f,则f=f0+△f。
依题意,该声波的波长λ声=0.5v声=0.5×320m=160m,则
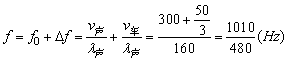 , ,
故5min内列车中的人能听到的钟声次数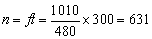 (次)。 (次)。
答案:631次。
例5、黄冈中学科技广场呈现圆形,半径为R=45m,如图,在主席台A与圆心O处各有一高音喇叭,发出频率相同的声波,波长为λ=10m,一人沿圆周走一圈,可听到声音最弱点共有几处?
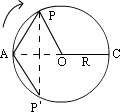
解答:
由图可知,P与P′处波程差为零,为加强点,再往前走,波程差可变为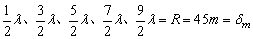 ,即A、C为弱点,故整个圆周上共有18处弱点,整个会场上将过这18个点作等位线可定其它减弱区域。 ,即A、C为弱点,故整个圆周上共有18处弱点,整个会场上将过这18个点作等位线可定其它减弱区域。
答案:18
|