一周强化

一、一周知识概述

　　主要复习为内容棱柱与棱锥、多面体、欧拉公式与球以及空间向量．了解棱柱、棱锥的概念，区别棱柱、直棱柱、正棱柱等概念；了解球的概念和性质，掌握球的表面积、体积公式，掌握它们的性质，理解空间向量概念，了解空间向量基本定理，会进行空间向量的运算，用空间向量解决空间的角、距离等问题。

二、本周学习重点和难点剖析

1、本周学习重点

（1）棱柱的分类：

　　

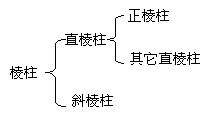
（2）棱柱的主要性质：

　　 ①侧棱都相等，侧面是平行四边形；

　　 ②两个底面与平行于底面的截面是全等的多边形；

　　 ③过不相邻的两条侧棱的截面是平行四边形．

（3）棱锥的主要性质

　　①棱锥被平行于底面的平面所截，那么截面和底面相似，并且它们面积比等于截得的棱锥的高和已知棱锥的高的平方比．

　　②正棱锥各侧棱长相等，各侧面都是全等的等腰三角形．

　　③正棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形；

　　正棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形．

（4）球面距离，是指经过球面上过这两点的大圆在这两点间的一段劣孤的长．

（5）空间向量的重要性主要体现它的工具性，利用空间向量解决立体几何中一些问题所体现的快捷性、灵活性和实用性．是其它数学方法无法比拟的，如利用空间向量证明直线与平面垂直的判定定理就是很好的例证．在学习中，应强化运用向量解决问题的意识，在向量使用中充分培养利用向量代数运算进行推理的能力，充分利用空间向量知识，重点解决空间圆形中的平行、垂直、角和距离等问题．

2、本周学习难点

　　（1）难点之一是以棱柱、棱锥为载体的一些计算或证明题．学习中，除了牢固的把棱柱、棱锥的有关概念和性质、面积公式掌握好以外，还要灵活地运用有关知识进行位置关系的判断与论证．

　　（2）难点之二是建立空间直角坐标系，解决有关的立体几何问题．空间向量的坐标运算，为解决立体几何问题提供有力的工具：夹角公式可求解立体几何中“线线”“线面成角问题”；空间两点间距离公式可计算空间线段的长度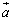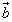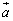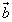：⊥，∥为证明线线平行，线线垂直等问题带来了方便．

例1、如图，在三棱锥P－ABC中，AB⊥BC，AB＝BC＝kPA，点O、D分别是AC、PC的中点，OP⊥底面ABC．

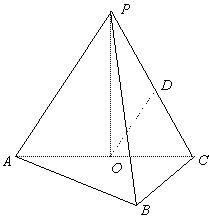
　　(Ⅰ)求证：OD∥平面PAB；

　　(Ⅱ)当k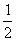＝时，求直线PA与平面PBC所成角的大小；

　　(Ⅲ) 当k取何值时，O在平面PBC内的射影恰好为△PBC的重心？

[解析]

例2、设正三棱锥P—ABC的底面边长为a，侧棱长为2a.过A作与PB、PC分别交于D、E的截面．

　　（1）求截面三角形ADE的周长的最小值；

　　（2）求截面三角形ADE周长最小时的截面面积．

[解析]

例3、如图，A、B、C是表面积为48π的球面上三点，AB=2，BC=4，∠ABC=60°，O为球心，则直线OA与截面ABC所成的角是(　)

[解析]

例4、如图，在四棱锥P—ABCD中，底面ABCD是矩形，侧棱PA⊥平面ABCD，E、F分别是AB、PC的中点．

　　(1)求证：CD⊥PD；

　　(2)求证：EF∥平面PAD；

　　(3)当平面PCD与平面ABCD成多大角时，直线EF⊥平面PCD？

[解析]