|
一周强化
一、知识方法概要
利用数学知识解决实际应用问题,是学习数学的一个重要的目的,也是高考的热点题型之一,这类题目主要考查学生如何将一个用文字语言叙述的应用题,概括、抽象为一个纯粹的数学化问题,如何抓住命题中所蕴涵的数学信息,恰当、准确地转化为一个数学模式是这类问题的关键.
1、高考中的实际应用题可以概括为三种类型:
一是由课本或其他书籍资料中原题改编的、与实际生活相关的应用题;
二是与横向学科(如物理、化学等)有联系的应用问题;
三是从社会热点出发,有实际生活背景、立意新颖的数学问题.
2、要顺利解决数学应用问题,首先应多接触社会、关注人口、土地、资源、环境、经济、销售、生产、交通、道路等热点问题;其次解答一个实际应用题要读懂题意,能将“问题情景”的文字语言转化为数学的符号语言,用数学式子表达关系.构建数学模型的过程中,要求学生有对数学知识的检索能力,认定或构建相应的数学模型,完成由实际问题向数学问题的转化.然后再用数学知识解答.这其中较难把握的是“问题情景的数学化”,因此要强化训练“理解语言能力”和“数学抽象化能力”.
一般来说:解决应用题的思路与方法:
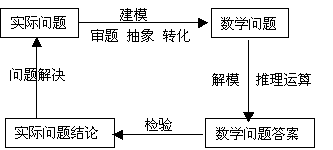
(1)审题:分为“读懂”和“加深理解”两个层次,把“问题情景”译为数学语言,找出问题的主要关系(目标与条件的关系)
(2)建模:把问题的主要关系近似化、形式化,抽象成数学问题.
(3)解模:把数学问题化归为常规问题,选择合适的数学方法求解.
(4)检验:对结果进行验证或评估,对错误加以调节,最后将结果应用于现实,作出解释或预测.
二、典型例题选讲
例1、某化妆品生产企业为了占有更多的市场份额,拟在2002年度进行一系列促销活动,经过市场调查和测算,化妆品的年销量x万件与年促销t万元之间满足3-x与t+1成反比例,如果不搞促销活动,化妆品的年销量只能是1万件,已知2002年生产化妆品的设备折旧,维修等固定费用为3万元,每生产1万件化妆品需再投入32万元的生产费用,若将每件化妆品的售价定为:其生产成本的150%“与平均每件促销费的一半”之和,则当年生产的化妆品正好能销完.
(Ⅰ)将2002年的利润y(万元)表示为促销费t(万元)的函数;
(Ⅱ)该企业2002年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入—生产成本—促销费,生产成本=固定费用+生产费用)
分析:
将利润y(万元)表示为促销费t(万元)的函数,可以利用利润=销售收入—生产成本—促销费建立其关系式;求促销费投入多少万元时,企业的年利润最大可以利用二次函数的单调性求解.
解:
(Ⅰ)由题意: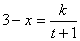 将 将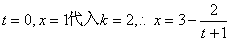
当年生产x(万件)时,年生产成本=年生产费用+固定费用
=32x+3=32(3-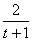 )+3, )+3,
当销售x(万件)时,年销售收入=150%[32(3-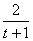 +3]+ +3]+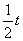
由题意,生产x万件化妆品正好销完
∴年利润=年销售收入-年生产成本-促销费
即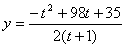 (t≥0) (t≥0)
(Ⅱ)∵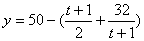 ≤50- ≤50-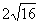 =42万件 =42万件
当且仅当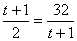 即t=7时,ymax=42 即t=7时,ymax=42
∴当促销费定在7万元时,利润增大.
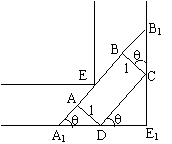
例2、一条直角走廊宽1.5米,如图所示,现有一转动灵活的手推车,其平板面的矩形宽为1米,问要想顺利推过直角走廊,平板车的长度不能超过多少米?
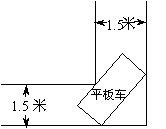
分析:
设角将有关线段用三角函数表示,利用三角函数的有界性和函数的单调性得到最大长度.
解:
如图,延长AB交直角走廊于A1、B1,设∠CDE1=q,则∠B1A1E1=q,q∈(0,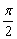 ), ),
∵CD=AB=A1B1-AA1-BB1,
而A1B1=1.5(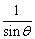 + +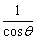 ),AA1=cotq,BB1=tanq, ),AA1=cotq,BB1=tanq,
∴CD=1.5(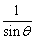 + +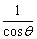 )―cotq―tanq= )―cotq―tanq=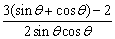 . .
令sinq+cosq=t,则t∈(1,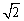 ].令f(t) ].令f(t)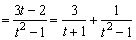 , ,
则当t=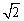 时,两项均取得最小值,即q= 时,两项均取得最小值,即q=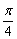 时, 时,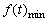 =3 =3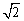 -2, -2,
即CDmin=3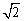 -2,故平板车的长度不能超过3 -2,故平板车的长度不能超过3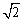 -2米. -2米.
例3、某城市为改善交通状况,需要进行路网改造.已知原有道路a个标段(注:1个标段是指一定长度的机动车道),拟新建x个标段道路和n个道路交叉口,n与x满足关系式n=ax+b,其中b为常数.设新建1个标段道路的平均造价为k万元,新建1个道路交叉口的平均造价是新建1个标段道路的平均造价的β倍(β≥1),n越大路网越畅通,记路网的堵塞率为μ,它与β的关系为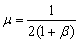 . .
(1)写出新建的道路交叉口的总造价y(万元)与x的函数关系式;
(2)若要求路网的堵塞率介于5%与10%之间(包含5%与10%),而且新建道路标段数为原有道路标段数的25%,求此时新建道路的总造价与新建道路交叉口的总造价之比P的取值范围(结果用a、b表示);
(3)若b=4,a变化时,在(2)的假设下,求使路网最畅通时,造价比p的最大值.
分析:总造价=平均造价×标段道路数(或道路交叉口数)
解析:
(1)由题意可得:y=kβ(ax+b)
(2)因为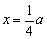 ,所以 ,所以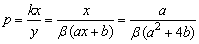
因为0.05≤μ≤0.1,则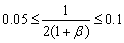 ,所以4≤β≤9 ,所以4≤β≤9
即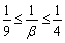 ,故p的取值范围是 ,故p的取值范围是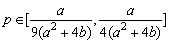
(3)要使路网最通畅,即β=9,又因为b=4,所以
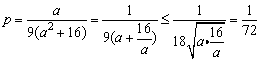
(当且仅当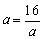 时等号成立). 时等号成立).
所以造价比的最大值为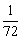 . .
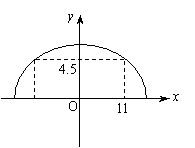
例4、如图,某隧道设计的双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状.
(1)若最大拱高h高6米,则隧道设计的拱宽l是多少?
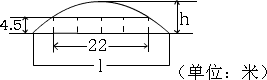
(2)若最大拱高h不小于6米,则应如何设计拱高h和拱宽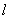 ,才能使半个椭圆形隧道的土方工程量最小? ,才能使半个椭圆形隧道的土方工程量最小?
(半个椭圆的面积公式为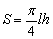 ,柱体体积为底面积乘以高,本题结果均精确到0.1米) ,柱体体积为底面积乘以高,本题结果均精确到0.1米)
分析:
可构造椭圆模型解题,因此要建立直角坐标系.
解答:
(1)建立恰当的直角坐标系,如图,先求椭圆的标准方程,只需两个独立条件,题设恰好提供了两个条件.
(2)利用重要不等式求解
由椭圆方程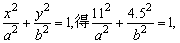
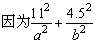 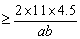 ,即ab≥99,且l=2a,h=b, ,即ab≥99,且l=2a,h=b,
所以,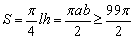 . .
当S取最小值时,有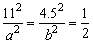 . .
得
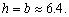
答:
(1)拱宽为约33.3米;
(2)当拱高约为6.4米,拱宽约为31.1米时,土方工程最小.
|