|
一周强化
一、知识精析
函数与方程思想是中学数学的基本思想,也是历年高考的重点.
函数思想,是用运动、变化的观点,集合与对应的思想,去分析和研究具体数学问题中的数量关系,通过建立函数关系或构造函数,运用函数的图象和性质去分析问题、转化问题,从而使问题获得解决.
方程思想,就是分析数某些数学问题中的变量间的等量关系,根据题设本身总量间的制约,列出等式,所设未知数沟通了变量之间的关系,从而建立方程或方程组,或者构造方程,通过解方程或方程组,或者运用方程的性质去分析、转化问题,使问题获得解决的一种思想方法。
函数与方程是两个不同的概念,但它们之间有着密切的联系,一个函数若有解析表达式,那么这个表达式就可以看成是一个方程,一个一元方程,它的两端可以分别看成函数。因此,许多有关方程的问题可用函数的方法解决;反之,许多有关函数的问题也可以用方程的方法解决。
函数思想的应用:(1)在求变量的取值范围时,考虑能否把该变量表示为另一变量的函数,从而转化为求该函数的值域;(2)构造函数是函数思想的重要体现;(3)运用函数思想要抓住事物在运动过程中那些保持不变的规律和性质,从而更快更好地解决问题。
运用方程思想解题时应注意的问题:(1)公式可以理解为方程(或等量关系)。于是,恒等式证明可以理解为方程变形,求值问题可以看成解方程问题;(2)曲线方程的确定及其位置关系的讨论,本质上就是方程(组)的求解或方程的根在某一实数区间的充要条件的确定;(3)函数的许多性质可以归纳为对方程的研究。
函数与方程的思想方法在高考中是常考的思想方法之一.函数与不等式也可以相互转化,它涉及到数学中的各分支.就中学数学而言,函数思想在解题中的应用主要表现在两个方面:一是借助有关初等函数的性质,解有关求值、解(证)不等式、解方程以及讨论参数的取值范围等问题;二是在问题的研究中,通过建立函数关系式或构造中间函数,把所研究的问题转化为讨论函数的有关性质,达到化难为易,化繁为简的目的.高考中涉及函数与方程思想的问题既出现在选择题、填空题上,还出现在解答题上。能全面考查思维的深刻性,并增强解决问题的创新意识和能力。
二、典型例题讲解
例1、设f(x)是定义在(-∞,3]上的减函数,已知f(a2-sinx)≤f(a+1+cos2x)对于x∈R恒成立,求实数a的取值范围.
分析:
本题应在定义域和增减性的条件下去掉函数符号f,使a从f中解脱出来.
解:
原式等价于a+1+cos2x≤a2-sinx≤3对x∈R恒成立
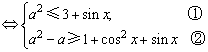 对x∈R恒成立 对x∈R恒成立
令t(x)=3+sinx,则①对x∈R恒成立
 a2≤tmin(x)=2 ③ a2≤tmin(x)=2 ③
令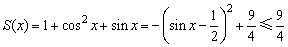
则②对x∈R恒成立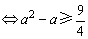 ④ ④
由③④可得所求实数a的取值范围是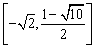 . .
说明:
在有关不等式的问题中要区别以下命题:
(1)a>f(x)恒成立 a>fmax(x). a>fmax(x).
(2)a<f(x)恒成立 a<fmin(x). a<fmin(x).
(3)a>f(x)有解 a>fmin(x). a>fmin(x).
(4)a<f(x)有解 a<fmax(x). a<fmax(x).
例2、(1)已知数列{an}中,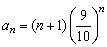 ,求an的最大值; ,求an的最大值;
(2)已知函数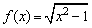 (x≥1)的反函数为f-1(x),在数列{an}中,a1=1,an=f-1(an-1)(n∈N*),求数列{bn}的通项公式. (x≥1)的反函数为f-1(x),在数列{an}中,a1=1,an=f-1(an-1)(n∈N*),求数列{bn}的通项公式.
分析:
(1)欲求{an}的最大值,可先确定数列{an}的单调性,只须比较an与an+1的大小即可.
(2)要求bn的通项公式,可先确定an与an-1的递推关系.
解:
(1)∵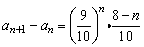 , ,
∴当1≤n≤8(n∈N*)时,{an}是递增的;
当n≥9(n∈N*)时,{an}是递减的.
∴最大值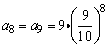 . .
(2)∵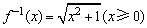 , ,
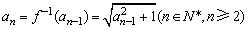
∴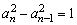 . .
又a1=1,∴{bn}是首项为1,公差为1的等差数列.
∴bn =n.
评注:
数列是一类特殊的函数,在解决某些数列问题时,可借助函数知识和方法求解.
例3、如图所示过椭圆C: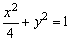 的右焦点,作一直线l交椭圆C于M、N两点,且M、N到直线 的右焦点,作一直线l交椭圆C于M、N两点,且M、N到直线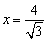 的距离之和为 的距离之和为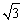 ,求直线l的方程. ,求直线l的方程.
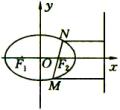
分析:
(1)先求椭圆的右焦点;(2)运用弦长公式和椭圆的定义两种途径求弦长|MN|,建立方程求l的斜率k;(3)由点斜式写出l的方程.
解:
∵椭圆C的右焦点F2为(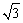 ,0),右准线为 ,0),右准线为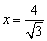 ,离心率 ,离心率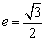 . .
∴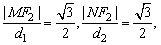 其中d1、d2分别为M、N到右准线的距离. 其中d1、d2分别为M、N到右准线的距离.
∵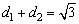 , ,
∴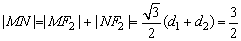 . .
设l: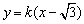
由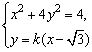 消去y整理得 消去y整理得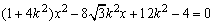 . .
设M(x1,y1),N(x2,y2),则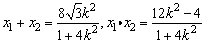
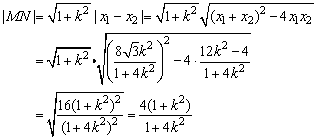
∵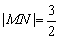 ,∴ ,∴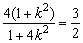 .解得 .解得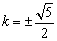 . .
∴所求直线l的方程为: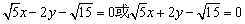 . .
评注:方程思想是处理直线与二次曲线有关问题的基本方法.
例4、设函数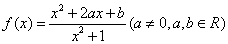 ,证明: ,证明:
(1)存在二实数m1,m2(m1<m2)满足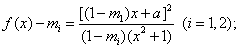
(2)对于(1)中的m1,m2,有m1≤f(x)≤m2(m1≤m2).
分析:
(1)即要证对任意x∈R,存在两个不同的m值,使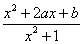 -m= -m=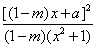 恒成立,(2)即证函数的值域是(1)中求出的m1,m2决定的区间[m1,m2]. 恒成立,(2)即证函数的值域是(1)中求出的m1,m2决定的区间[m1,m2].
解:
(1)由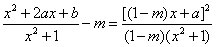 ,得 ,得
(1-m)[x2+2ax+b-m(x2+1)]=[(1-m)x+a]2,
∴m2-(b+1)m+b-a2=0.
∵ △=(b+1)2-4(b-a2)=(b-1)2+4a2>0.
∴必存在两个实数m1,m2,即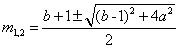 ,使等式成立. ,使等式成立.
(2)令y=f(x),则(x2+1)y=x2+2ax+b,∴x2(1-y)+2ax+b-y=0.
∵x∈R,∴△=4a2-4(b-y)(1-y)≥0,
即y2-(b+1)y+b-a2≤0,即m1≤y≤m2.
反思:
曲线方程的确定及曲线位置关系的讨论,本质上就是方程(组)的求解或方程的根在某一实数区间的充要条件的确定。
|