本大节的重点是根据导数定义求简单函数的导数的方法. 利用导数判别可导函数极值的方法．
利用导数的符号判断函数的增减性及极（最）值：
极值和最大（小）值的判定，其中关键是可导函数极值的判定，通过判定可导函数的极值，可加深对可导函数单调性与其导数的关系的了解；并且，掌握了可导函数极值的判别法，再学习可导函数最大（小）值的判定，就不成问题了．
（1）研究函数的单调性：设函数y=f(x)在某区间可导，若f′(x)>0，则f(x)为增函数；若f′(x)＜0，则f(x)为减函数；如果f′(x)=0，则f(x)为常值函数.
（2）研究函数的极（最）值：设函数在点x0附近有定义，如果对x0附近所有的点，都有f(x)>f(x0)（或f(x)<f(x0)），我们就说f(x0)是函数f(x)的一个极大值（或极小值）.若x0是f(x)的一个极值点，且f(x)是可导函数，则f′(x0)=0，如果函数f(x)在点x0处连续，且f′(x)在x0的两侧异号，那么x0就是函数f(x)的极值点.
（3）函数f(x)在[a，b]上最大值与最小值的求法.
①求出f(x)在（a，b）内的极值；
②将各极值与f(a)，f(b)比较，其中最大的一个为最大值，最小的一个为最小值.
难点是对导数概念的理解和导数的应用.
导数是建立在极限基础上，并用极限定义的基本概念，它在微积分中有极其重要的地位，导数即函数的变化率，它可直接反映出许多实际问题中函数变化的快慢程度，所以学习时要善于联系导数概念的某些实际背景（例如瞬时速度，加速度，光滑曲线的切线的斜率等）. 利用导数的符号判断函数的增减性，是导数几何意义在研究曲线变化规律时的一个应用，它充分体现了数形结合的思想.
导数的方法涉及导数定义、常用求导公式、四则运算法则和复合函数求导法则等求导方法，因此重点应为导数的概念与计算，学习时应熟练掌握以下求导法：直接利用法则与公式求导、复合函数求导．在求导过程中应熟记导数公式与运算法则，重点掌握复合函数的求导方法. 求一些实际问题的最大值与最小值是本大节的难点，在掌握可导函数极值的判别法之后，判定可导函数的最大（小）值并不困难，但在遇到一些实际问题时，可能会出现障碍，这里关键是能根据实际问题，建立适当的函数关系.
1、导数的定义
设函数y=f(x)在点x=x0及其附近有定义，当自变量x在x0处有改变量△x（△x可正可负），则函数y相应地有改变量△y=f(x0＋△x)－f(x0)，这两个改变量的比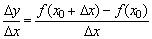
叫做函数y=f(x)在x0到x0＋△x之间的平均变化率.
如果当△x→0时，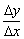
有极限，我们就说函数y=f(x)在点x0处可导，这个极限叫做f(x)在点x0处的导数（即瞬时变化率，简称变化率），记作f′(x0)或
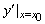，即
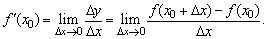
函数f(x)在点x0处的导数就是函数平均变化率当自变量的改变量趋向于零时的极限．如果极限不存在，我们就说函数f(x)在点x0处不可导.
2、求导数的方法
由导数定义，我们可以得到求函数f(x)在点x0处的导数的方法：
（1）求函数的增量△y=f(x0＋△x)－f(x0)；
（2）求平均变化率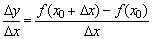
；
（3）取极限，得导数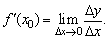
3、导数的几何意义
函数y=f(x)在点x0处的导数的几何意义，就是曲线y=f(x)在点P（x0，f(x0)）处的切线的斜率f′(x0).
相应地，切线方程为y－y0= f′(x0)(x－x0).
4、几种常见函数的导数
函数y=C（C为常数）的导数 C′=0.
函数y=xn（n∈Q）的导数 (xn)′=nxn－1
函数y=sinx的导数 (sinx)′=cosx
函数y=cosx的导数 (cosx)′=－sinx
5、函数四则运算求导法则
和的导数 (u＋v)′=u′＋v′
差的导数 (u－v)′= u′－v′
积的导数 (u·v)′=u′v＋uv′
商的导数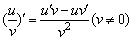 
.
6、复合函数的求导法则
一般地，复合函数y=f[φ(x)]对自变量x的导数y′x，等于已知函数对中间变量u=φ(x)的导数y′u，乘以中间变量u对自变量x的导数u′x，即y′x=y′u·u′x.
7、对数、指数函数的导数
（1）对数函数的导数
①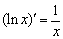
；
②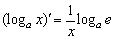
.
其中（1）式是（2）式的特殊情况，当a=e时，（2）式即为（1）式.
（2）指数函数的导数
①(ex)′=ex
②(ax)′=axlna
其中（1）式是（2）式的特殊情况，当a=e时，（2）式即为（1）式.
［例1］求下列函数的导数：
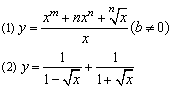
分析：
从这两个函数的形式结构来看，都是商的形式，如果直接套用商的求导法则，运算量较大，但从形式上看，可以转化为和的形式.
解：
（1）
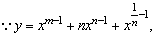
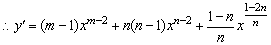
（2）
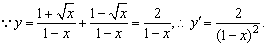
点评：
（1）不加分析，盲目套用公式，会给运算带来不便，甚至错误，如（2）的求导形式较为复杂，用商的求导法则之后，还需通分化简.
（2）先化简，再求导实施求导运算的基本方法，是化难为易、化繁为简的基本原则和策略．
［例2］已知f(x)的导数f′(x)=3x2－2(a＋1)x＋a－2且f(0)=2a，求不等式f(x)<0的解集.
分析：
欲求f(x)<0的解集，必须根据条件先确定f(x)的表达式，逆用导数运算法则，可得f(x)=x3－(a＋1)x2＋(a－2)x＋b，确定a，b值即可.
解：
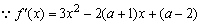
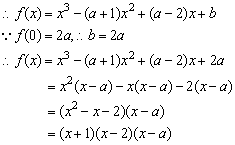
令(x＋1)(x－2)(x－a)<0，则：
（1）当a<－1时，不等式解集为（－∞，a）∪（1，2）
（2）当a=－1时，不等式解集为（－∞，－1）∪（－1，2）
（3）当－1<a<2时，不等式解集为（－∞，－1）∪（a，2）
（4）当a=2时，不等式解集为（－∞，－1）；
（5）当a>2时，不等式解集为（－∞，－1）∪（2，a）
点评：
已知导数求原函数的法则，是导数运算法则的逆用，可以培养逆向思维能力，应加注意，根据导数求原来函数时，不是惟一的，这是因为常数的导数为0的缘故.
[例3] 如果函数f(x)=ax5－bx3＋c（a≠0）在x=±1时有极值，极大值为4，极小值为0，试求a，b，c的值.
[分析]
可通过求导确定可疑点，注意利用已知极值点x=±1所确定的相关等式，在判断y′的符号时，必须对a进行分类计论.
[解答]
y′=5ax4－3bx2，令y′=0，即5ax4－3bx2=0,x2(5ax2－3b)=0，
∵ x=±1是极值点，∴ 5a(±1)2－3b=0.
又x2=0，∴ 可疑点为x=0，x=±1.
若a>0，y′=5ax2(x2－1).
当x变化时，y′，y的变化情况如下表：
为多大时，才能使横断面被水浸湿的长度(称为湿周)最小?并求出最小湿周.
，
则
∴
;令
则
∴
,
时，可使湿周最小，最小值为