|
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.
第Ⅰ卷(选择题,共50分)
一、选择题(本大题共10小题,每小题5分,共50分.每小题给出的四个选项中,只有一项是符合题目要求.)
1、已知数列1,3,6,10,…,则它的一个通项公式是( )

2、已知数列an=an+m(a<0,n∈N*),且a1=2,a2=4,则a3的值为( )
A.6 B.8
C.2 D.9
3、已知等差数列{an}的前三项依次是a-1,a+1,2a+3,则此数列的通项an为( )
A.2n-5 B.2n-3
C.2n-1 D.2n+1
4、若{an}为等差数列,且a3,a10是方程x2-3x-5=0的两根,则a5+a8等于( )
A.-5 B.5
C.-3 D.3
5、设Sn是等差数列{an}的前n项和,若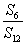 等于( ) 等于( )
A.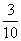 B. B.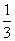
C.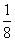 D. D.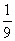
6、公差不为0的等差数列的第2、第3、第6项构成等比数列,则其公比为( )
A.1 B.2
C.3 D.4
7、已知等比数列{an}的首项为1,公比为q,前n项之和为S,则数列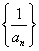 的前n项之和是( ) 的前n项之和是( )
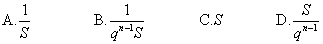
8、已知数列{an}是等比数列,记bn=an+an+1(n∈N*),则数列{bn}( )
A.是等比数列,但不是等差数列
B.是等差数列,但不是等比数列
C.既可能是等差数,也可能是等比数列
D.既不是等比数列,也不是等差数列
9、某工厂在2000年底制定计划,要使 的总产值在2000年的基础上翻三番,则年平均增长率为( )

10、等差数列{an}的公差为d,前n项的和为Sn,当首项a1和d变化时,a2+a8+a11是一个定值,则下列和数中也为定值的是( )
A.S7 B.S8
C.S13 D.S15
[提示]
第Ⅱ卷(非选择题,共100分)
二、填空题(本大题共5小题,每小题5分,共25分.)
11、数列{an}满足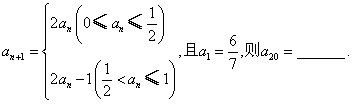
12、已知整数对序列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…,则第60个数对为_____________.
13、若数列{an}是等差数列,且a1>0,a23+a24>0,a23·a24<0,则使前n项和Sn>0成立的最大的自然数n是_______________.
14、设等比数列{an}的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为______________.
15、假如你在某公司打工,老板给你两个加薪方案:(1)每年年末加1000元;(2)每半年结束时加300元.如果每个人的加薪方案只选一种,并且在该公司至少干三年,那么最终收入高的加薪方案是________________.
[答案]
三、解答题(本大题共6小题,共75分.解答时应写出必要的文字说明,证明过程或演算步骤.)
16、(本小题满分12分)已知{an}为等比数列,且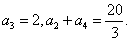 求{an}的通项公式. 求{an}的通项公式.
[答案]
17、(本小题满分12分)已知等比数列{an}及等差数列{bn},其中b1=0,公差d≠0,将这两个数列的对应项相加,得一新数列1,1,2,…,试求这个新数列的前10项之和.
[答案]
18、(本小题满分12分)数列{an}的首项为a1=1,前n项和Sn满足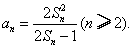
(1)求前n项和Sn;
(2)求数列{an}的通项公式.
[答案]
19、(本小题满分12分)我国北方地区发生的多起沙尘暴,主要是由于土地沙漠化引起的.据调查,北方某县2005年底有一定面积(单位:亩)的沙漠,以后每年被沙漠化的土地面积相同,该县从2006年起在沙漠上植树,改造沙漠为森林,以后每年都比上一年多植相同面积的树木改造沙漠.据统计,沙漠总面积及每年植树面积如图4-1所示,问到哪一年年底可以将所有的沙漠改造完?
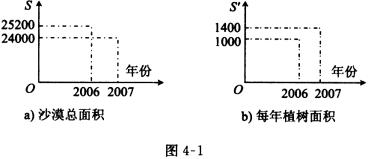
[答案]
20、(本小题满分13分)已知f(x)=(x-1)2,g(x)=4(x-1),数列{an}满足a1=2,(an+1-an)g(an)+f(an)=0.
(1)用an表示an+1;
(2)求证:数列{an-1}是等比数列;
(3)若bn=3f(an)-g(an+1),求数列{bn}的最大项和最小项.
[答案]
21、(本小题满分14分)一个公差不为0的等差数列{an}共有100项,首项为5,其第1,4,16项分别为正项等比数列{bn}的第1,3,5项.
(1)求数列{an}各项的和S;
(2)若数列{bn}的末项不大于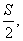 求数列{bn}的项数的最值N; 求数列{bn}的项数的最值N;
(3)设数列{an}的前n项和为Sn,数列{bn}的前n项和为Tn,问是否存在自然数m,使得Sm=TN?证明你的结论.
[答案]
|