高考第一轮 数学(理科)
单元训练题五 三角函数(1)
|
|
本试卷分第Ⅰ卷和第Ⅱ卷两部分,共150分,考试时间120分钟.
第Ⅰ卷(选择题,共50分)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个符合题目要求.)
1、已知简谐运动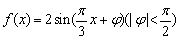 的图像经过点(0,1),则该简谐运动的最小正周期T和初相 的图像经过点(0,1),则该简谐运动的最小正周期T和初相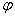 分别为( ) 分别为( )

2、已知cosθ·tanθ<0,那么角θ是( )
A.第一或第二象限角 B.第二或第三象限角
C.第三或第四象限角 D.第一或第四象限角
3、函数y=|sinx|的一个单调增区间是( )

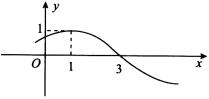
4、函数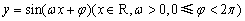 的部分图像如图所示,则( ) 的部分图像如图所示,则( )

5、已知cos31°=m,则sin239°·tan149°的值是( )

6、若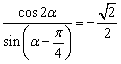 ,则cosα+sinα的值为( ) ,则cosα+sinα的值为( )

7、设x是实数,且满足等式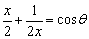 ,则实数θ等于( ) ,则实数θ等于( )
A.2kπ(k∈Z) B.(2k+1)π(k∈Z)
C.kπ(k∈Z) D.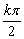 (k∈Z) (k∈Z)
8、在△ABC中,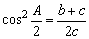 ,则△ABC为( ) ,则△ABC为( )
A.直角三角形
B.等腰三角形或直角三角形
C.正三角形
D.等腰直角三角形
9、若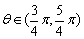 ,则复数(cosθ+sinθ)+(sinθ-cosθ)i在复平面内所对应的点在( ) ,则复数(cosθ+sinθ)+(sinθ-cosθ)i在复平面内所对应的点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
10、设两个向量a=(λ+2,λ2-cos2α)和b=(m,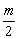 +sinα),其中λ,m,α为实数.若a=2b,则 +sinα),其中λ,m,α为实数.若a=2b,则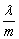 的取值范围是( ) 的取值范围是( )
A.[-6,1] B.[4,8]
C.(-6,1] D.[-1,6]
[提示]
第II卷(非选择题,共100分)
二、填空题(本大题共5小题,每小题5分,共25分.)
11、若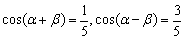 ,则tanαtanβ=______________. ,则tanαtanβ=______________.
12、已知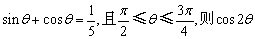 的值是______________. 的值是______________.
13、设α为第四象限的角,若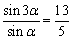 ,则tan2α=______________. ,则tan2α=______________.
14、函数f(x)=sinx+2|sinx|,x∈[0,2π]的图像与直线y=k有且仅有两个不同的交点,则k的取值范围是__________.
15、下面有五个命题:
①函数y=sin4x-cos4x的最小正周期是π;
②终边在y轴上的角的集合是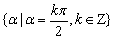 ; ;
③在同一坐标系中,函数y=sinx的图像和函数y=x的图像有三个公共点;
④把函数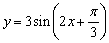 的图像向右平移 的图像向右平移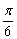 得到y=3sin2x的图像; 得到y=3sin2x的图像;
⑤函数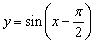 在[0,π]上是减函数. 在[0,π]上是减函数.
其中真命题的序号是____________.(写出所有真命题的序号)
[答案]
三、解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.)
16、(本小题满分12分)已知函数f(x)=2sinx·(sinx+cosx).
(1)求函数f(x)的最小正周期和最大值;
(2)在给出的直角坐标系中,画出函数y=f(x)在区间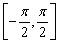 上的图像. 上的图像.
[答案]
17、(本小题满分12分)已知函数f(x)=sin(ωx+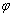 )(ω>0,0≤ )(ω>0,0≤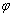 ≤π)是R上的偶函数,其图像关于点 ≤π)是R上的偶函数,其图像关于点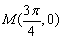 对称,且在区间 对称,且在区间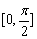 上是单调函数.求 上是单调函数.求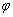 和ω的值. 和ω的值.
[答案]
18、(本小题满分12分)设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA.
(1)求B的大小;
(2)求cosA+sinC的取值范围.
[答案]
19、(本小题满分12分)设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx,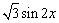 ),x∈R. ),x∈R.
(1)若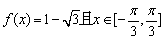 ,求x; ,求x;
(2)若函数y=2sin2x的图像按向量c=(m,n)(|m|<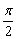 )平移后得到函数y=f(x)的图像,求实数m,n的值. )平移后得到函数y=f(x)的图像,求实数m,n的值.
[答案]
20、(本小题满分13分)如图所示,甲船以每小时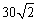 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20min到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20min到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距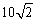 海里,问乙船每小时航行多少海里? 海里,问乙船每小时航行多少海里?
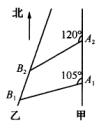
[答案]
21、(本小题满分14分)已知奇函数f(x)的定义域为R,且f(x)在[0,+∞)上是增函数,当0≤θ≤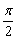 时,是否存在这样的函数m,使f(4m-2mcosθ)-f(2sin2θ+2)>f(0)对所有的θ∈[0, 时,是否存在这样的函数m,使f(4m-2mcosθ)-f(2sin2θ+2)>f(0)对所有的θ∈[0,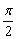 ]均成立?若存在,求出所有适合条件的实数m;若不存在,说明理由. ]均成立?若存在,求出所有适合条件的实数m;若不存在,说明理由.
[答案]
|